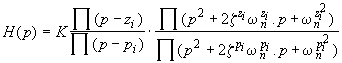Lien entre le diagramme de Bode et la fonction de transfert
On peut définir la fonction de transfert pour un système du
n-ième ordre en fonction des pôles et des zéros réels ou
complexes conjugués:
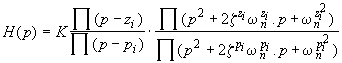
où pi, z i sont les pôles et les zéros
réels (simples ou multiples) et les autres termes ont pour
racines des pôles et des zéros complexes conjugués.
Diagramme de Bode pour les basses fréquences
Le nombre d'intégrateurs et le gain déterminent entièrement
le diagramme de Bode pour les basses fréquences.
Diagramme de Bode pour les hautes fréquences
Le nombre de pôles et de zéros définit le comportement
asymptotique du Diagramme de Bode aux hautes fréquences.
La valeur du module pour les hautes fréquences est:
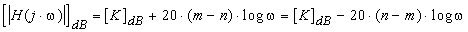
où n est le nombre de pôles et m le nombre de
zéros.
Le module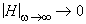 
si n>m avec une pente de:
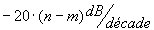
La valeur de la phase est égale à:
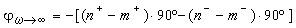
où n+ et m+
représentent le nombre de pôles / zéros dits
"stables", c'est à dire à partie réelle négative ou
nulle et n- et m- représentent le nombre
de pôles / zéros dits "instables", c'est à dire à
partie réelle strictement positive.
Dans le cas où tous les pôles et les zéros
sont à partie réelle négative ou nulle, n- = 0, m-
= 0, n+ = n et m+ = m, donc:
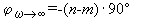
Démonstration
Diagramme de Bode pour les moyennes
fréquences
La valeur des pôles et des zéros définit le
diagramme de Bode pour les moyennes fréquences.
[ Table des matières ]