Représentation des zéros sur le diagramme de Bode
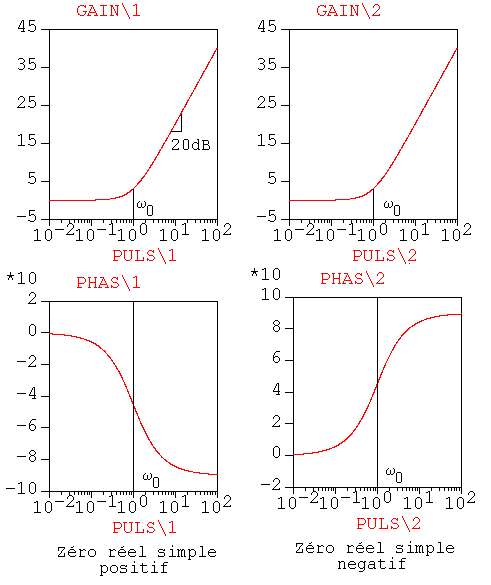
1) Dans le diagramme de Bode-Gain, un zéro réel simple négatif z0 est caractérisé par l'existence d'une rupture de pente des asymptotes; à partir de la pulsation :w0= çz0ç
le module de la réponse harmonique augmente de 20dB par décade.
Dans le diagramme de Bode-Phase, un zéro réel simple négatif z0 est caractérisé par une croissance de 90° sur toute la plage de pulsation. L'augmentation à w0= çz0ç est de 45°.
2) Dans le diagramme de Bode-Gain, un zéro réel simple positif z0 est caractérisé par l'existence d'une rupture de pente des asymptotes; à partir de la pulsation :
w0= z0
le module de la réponse harmonique croit de 20dB par décade.
Dans le diagramme de Bode-Phase, un zéro réel simple positif z0 est caractérisé par une décroissance de 90° sur toute la plage de pulsation. La diminution à w0= z0 est de 45°.
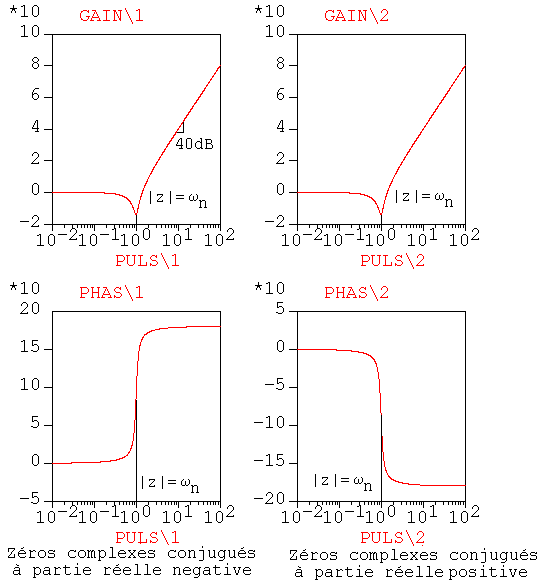
3) Dans le diagramme de Bode-Gain, une paire de zéros complexes conjugués de module wn, est caractérisée par l'existence d'une rupture de pente; à partir de la pulsation wn, le module de la réponse harmonique a une croissance de 40dB par décade.
Dans le diagramme de Bode-Phase, une paire de zéros complexes conjugués de partie réelle positive est caractérisée par une décroissance de 180°.
4) Dans le diagramme de Bode-Phase, une paire de zéros complexes conjugués de partie réelle négative est caractérisée par une croissance de 180°.