Il existe d'autres formulations que la réponse impulsionnelle pour représenter
les SLIT, par exemple sous la forme d'une équation différentielle
linéaire à coefficients constants. Ainsi l'évolution d'un
système du premier ordre comme la tension aux bornes d'un
condensateur de capacité 
(fig. 9) peut s'exprimer
en utilisant la représentation
 |
(9) |
La réponse impulsionnelle de ce système est obtenue en appliquant
à l'entrée une impulsion de Dirac. En supposant que 
pour
les temps négatifs, on trouve que
La valeur du coefficient multiplicatif (
) caractérisant l'amplitude de la
réponse impulsionnelle est obtenue en remplaçant l'impulsion de
Dirac par un créneau de longueur 
et de hauteur
. On résoud l'équation différentielle puis on fait
tendre vers 0.
Si le système est au repos ( pour 
), il est alors équivalent de résoudre
l'équation différentielle ou de calculer le résultat de la
convolution de l'entrée 
par 
. Il est aussi possible
de représenter les systèmes sous la forme de transformées de
Fourier ou de Laplace, ce que nous verrons dans le paragraphe
suivant.
Figure:
Exemple classique de système linéaire représenté par un filtre du premier ordre de réponse impulsionnelle
de forme exponentielle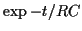 
 |
Ce calcul de moyenne met en évidence les fluctuations lentes (les fréquences basses) et atténue les
fluctuations rapides (les hautes fréquences).
[ Table des matières ]
