Les filtres à réponse impulsionnelle
infinie
Il est possible dans un cas particulier de réaliser des filtres
dont la réponse impulsionnelle a un nombre infini d'échantillons,
mais ceci nécessite l'expression de la sortie du filtre sous la
forme d'une équation récurrente liant 
aux échantillons
précédemment calculés
et aux échantillons
du signal d'entrée,
. Considérons par
exemple l'équation récurrente suivante, en supposant que les
valeurs des conditions initiales
sont
nulles:
 |
(129) |
On définit les polynômes
 |
(130) |
 |
(131) |
Si on connait la valeur de la transformée en 
de 
, on peut calculer la transformée en de
l'équation récurrente
 |
(132) |
qu'on peut aussi écrire
 |
(133) |
 |
(134) |
et en
remarquant que la valeur de la transformée en de l'opérateur
retard est 
on obtient
 |
(135) |
Dans le domaine des transformées en , la réponse du filtre
n'est plus un polynôme mais une fraction rationnelle. Dans ce cas
le filtre n'est pas toujours stable. Nous verrons dans un prochain
paragraphe une méthode pour analyser la stabiité d'un filtre
récursif (autre terme pour nommer les filtres à réponse
impulsionnelle infinie).
L'écriture complète de la transformée 
nécessite la
connaissance des valeurs des conditions initiales
,
que nous avions
supposées égales à zéro.
La transformée en du signal 
égal à 
pour 
et nul pour t<0 est données par la formule connue sous le nom du
théorème de l'avance
 |
(136) |
que nous noterons sous sous la forme
 |
(137) |
où 
est la transformée en du signal causal
.
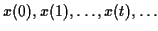De même
 |
(138) |
que nous noterons sous sous la forme
 |
(139) |
La transformée en de l'équation récurrente prenant en compte
les conditions initiales s'écrit
 |
(140) |
soit
|
(141) |
 |
(142) |
Les conditions initiales se traduisent par des modifications du
numérateur de la fonction de transfert mais ne modifient pas les
pôles qui, eux ne proviennent que des pôles de et 
.
Sous-sections
[ Table des matières ]