C'est une forme de filtre où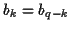 
. Si on calcule les
racines du polynôme 
, on remarque que si 
est racine,
alors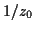 
est aussi racine.
Les positions possibles des racines sont données par la figure
34. Si elles sont complexes et de module différent de
un, elles se regroupent par quatre , 
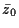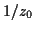, et
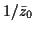. Sinon elles se trouvent ainsi que leur complexe
conjugué sur le cercle de rayon un.
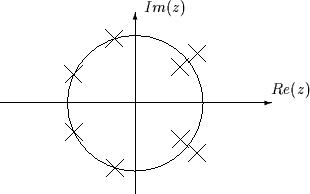
Figure 34:
Positions possibles des racines d'un filtre non récursif à réponse impulsionnelle réelle symétrique:
ces racines sont soit sur le cercle unité, soit regroupées par quadruplets avec leur inverse, leur conjugué et l'inverse de leur conjugué
 |
Si de plus on suppose que 
n'a pas de racines sur le cercle de rayon un, alors est un
réel (positif si 
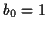). Dans ce cas le déphasage apporté par le
filtre est nul. C'est un filtre qui déforme relativement peu les
signaux. Ce type de filtre ne peut pas être réalisé
simplement en utilisant les technologies analogiques.
[ Table des matières ]