Lien entre le diagramme de Nyquist et la fonction de transfert
Soit la fonction de transfert: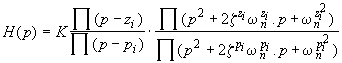
où pi, z i sont les pôles et les zéros réels (simples ou multiples) et les autres termes ont pour racines des pôles et des zéros complexes conjugués.
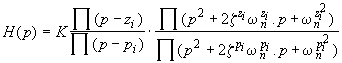
où pi, z i sont les pôles et les zéros réels (simples ou multiples) et les autres termes ont pour racines des pôles et des zéros complexes conjugués.
La valeur du module pour les hautes fréquences est:
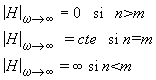
où n est le nombre de pôles et m le nombre de zéros.
La valeur de la phase est égale à:
![]()
où n+ et m+ représentent le nombre de pôles / zéros dits "stables", c'est à dire à partie réelle négative ou nulle et n- et m- représentent le nombre de pôles / zéros dits "instables", c'est à dire à partie réelle strictement positive.
Dans le cas où tous les pôles et les zéros sont à partie réelle négative ou nulle, n- = 0, m- = 0, n+ = n et m+ = m, donc:
![]()