Soit la fonction de transfert sous sa forme polynomiale:
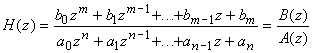
Le critère de Jury étudie la position des racines du polynôme caractéristique A(z), à l'intérieur du cercle unité.
Soit
,
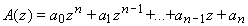avec
.
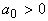On construit le tableau à 2n-3 lignes suivant:
Les premières lignes sont construites à partir des coefficients ai, du polynôme caractéristique A(z).
Les deux lignes suivantes sont construites à partir des deux
premières par
,
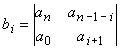puis les deux suivantes par:
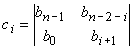
La condition nécessaire et suffisante de stabilité asymptotique est constituée des conditions suivantes qui doivent être remplies simultanément:
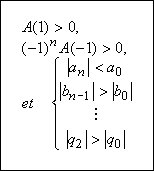
- Cas
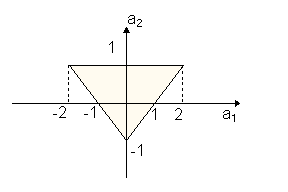
particulier: 2eme ordre
- Le polynôme caractéristique est:
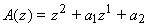
Les conditions du critère de Jury se ramènent dans ce cas particulier à :
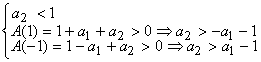
- Cas
particulier: 3eme ordre
- Le polynôme caractéristique est:
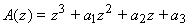
Le tableau de Jury est:
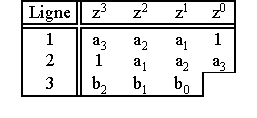
Les conditions du critère de Jury sont:
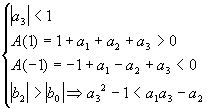
Critère modifié de Routh
- On utilise la
transformation
bilinéaire (homographique ou de Möbius) pour transformer le
polynôme caractéristique A(z) en A(w).
- On applique
le
critère de Routh sur le polynôme caractéristique
A(w).
- Remarque
Le critère de Routh indique le nombre exact de racines de A(w) qui sont situées dans le demi-plan droit du plan complexe ainsi que le nombre de racines situées sur l'axe imaginaire. Toutefois, dans un contexte de synthèse de commande cette information sur le nombre de pôles instables n'est pas nécessaire, car les systèmes en boucle fermée instables ou à la limite d'instabilité ne sont pas désirables.
Les calculs nécessaires à cette méthode sont plus complexes que ceux employés pour le critère de Jury, qu'il est préférable d'utiliser.