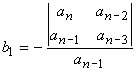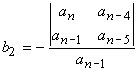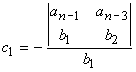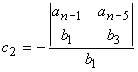Détermination de la stabilité à partir de la fonction de transfert d'un système
continu: le critère algébrique de Routh
Critère de Routh
Soit la fonction de transfert sous sa forme polynomiale:
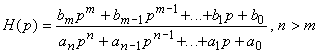
Soit le polynôme caractéristique:
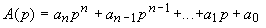
On construit le tableau suivant:
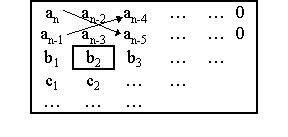
avec:
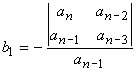
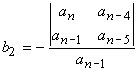
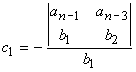
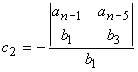
Enoncé du critère de Routh:
Le nombre de pôles à partie réelle positive est donné par
le nombre de changements de signe des termes de la première colonne.
Dans le cas où le tableau de Routh possède un élément nul
dans la première colonne alors:
- si la ligne correspondante contient un ou plusieurs éléments non-nuls,
A(p) possède au moins une racine à partie réelle strictement positive.
- si tous les éléments de la ligne sont nuls alors:
- A(p) a au moins une paire de racines imaginaires pures,
- ou A(p) possède une paire de racines réelles de signes opposés,
- ou A(p) possède quatre racines complexes conjuguées deux à deux
et de parties réelles de signes opposés deux à deux.
Remarque :
Une condition nécessaire mais non suffisante est que tous les coefficients du
polynôme caractéristique soient positifs.
Exemple : Soit le polynôme caractéristique A(p)= p3-2p2-13p-10
| p3 |
1 |
-13 |
| p2 |
-2 |
-10 |
| p |
-18 |
0 |
| p0 |
-10 |
|
Un changement de signe, donc un pôle instable. En effet, A(p) a pour racines -1,
-2, 5.
Exemple : Soit le polynôme caractéristique A(p)=p4+ p3+5p2+4p+4
| p4 |
1 |
5 |
4 |
| p3 |
1 |
4 |
0 |
| p2 |
1 |
4 |
|
| p |
e |
0 |
|
| p0 |
4 |
|
|
Deux racines imaginaires pures (+2j, -2j) ; les autres sont 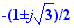 .
.
Exemple : Soit la fonction de transfert en boucle ouverte H(p)=K(p-1)/p(1+Tp) avec T>0. Le dénominateur
en boucle fermée est : Tp2+(1+K)p-K
Ce système est instable pour tous les gains positifs.
[ Table des matières ]
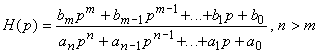
![]()