L'échantillonneur idéal

Définition

L'échantillonneur idéal prélève la valeur d'un signal analogique toutes les Te secondes; Te est appelée période d'échantillonnage.

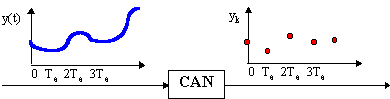
Du point de vue mathématique, l'échantillonneur idéal réalise la multiplication du signal originel par la fonction peigne de Dirac, paramétrée par Te.

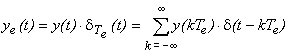
Le spectre du signal après l'échantillonnage idéal sera:

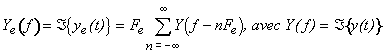
Pour reconstruire la composante de ce spectre correspondant à n=0, on utilise un filtre passe-bas idéal de bande passante Fe/2:

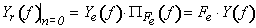
Après le filtrage idéal des basses fréquences, on obtient à un coefficient près, le spectre du signal originel si la condition de Shannon est respectée.