Influence du nombre d'intégrateurs en boucle ouverte sur la précision en asservissement d'un système en boucle fermée, à retour unitaire
Soit un schéma classique de système en boucle fermée:

Supposons qu'il n'existe pas de perturbation dans le système et que la consigne est de type polynomial, de transformée de Laplace :
![]()
où C est une constante.
Soit nI le nombre d'intégrateurs en boucle ouverte:
![]()
Le tableau suivant donne les erreurs statiques entre une consigne de type polynomial et la sortie du système, en fonction du nombre d'intégrateurs en boucle ouverte nI :
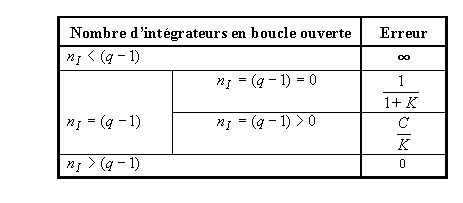
Pour les entrées les plus courantes, l'application de ce tableau donne :
|
nI |
0 |
1 |
2 |
|
Entrée échelon |
1/1+K |
0 |
0 |
|
Entrée rampe |
¥ |
1/K |
0 |
|
Entrée accélération |
¥ |
¥ |
1/K |
Attention !
Les résultats présentés dans ce tableau sont valables seulement si la limite du signal d'erreur entre la consigne et la sortie existe, c'est à dire si le système en boucle fermée est asymptotiquement stable. Il faut bien vérifier que les valeurs du gain en boucle ouverte et du nombre d'intégrateurs en boucle ouverte n'amènent pas le système en boucle fermée à l'instabilité.
Pour une explication, voir
