Détermination des constantes de temps à partir des pôles d'un système

  1. Relation entre la constante de temps et le pôle d'un système du premier ordre
  2. Détermination de la constante de temps équivalente d'un système du deuxième ordre avec z< 1 à partir de ses pôles
  3. Détermination de la constante de temps dominante d'un système du deuxième ordre avec z >> 1 à partir de ses pôles

  1. Relation entre la constante de temps et le pôle d'un système du premier ordre

      Le pôle d'un système du premier ordre stable (au sens de Lyapunov) est réel et négatif et égal à -1/T où T est la constante de temps du système.

  2. Détermination de la constante de temps équivalente d'un système du deuxième ordre avec

    z < 1 à partir de ses pôles
      La réponse oscillante d'un système du deuxième ordre avec z < 1 est bornée par son enveloppe exponentielle dont l'expression est .

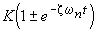      Les pôles sont:

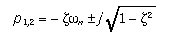
      Dans ce cas on peut définir une constante de temps équivalente (par analogie avec un système de premier ordre) : .

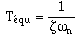      Elle peut être utilisée pour estimer la rapidité du système. Effectivement, on peut vérifier que le temps de réponse à 5% (respectivement 2%) est plus petit que 3Téqu (respectivement 4Téqu).

  3. Détermination de la constante de temps dominante d'un système du deuxième ordre avec

    z >> 1 à partir de ses pôles

      Lorsque z >>1, les pôles du système ont des valeurs réelles:


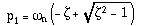
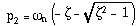
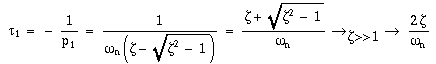
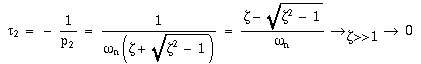
      A chaque pôle correspond une constante de temps:

      La constante de temps la plus lente,t1, est nommée dominante, parce qu'elle influence le plus le comportement transitoire du système. Dans ce cas, un système du deuxième ordre peut être approximé par un système du premier ordre de constante de temps T =t1.

    [ Table des matières ]