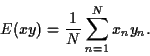Afin de simplifier la présentation, nous supposerons que les variables aléatoires sont centrées ce qui
peut pratiquement toujours s'obtenir en effectuant une
translation. La manière la plus élémentaire de caractériser une
éventuelle relation entre 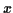 et
et 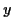 est de calculer les trois
moments du deuxième ordre des deux variables aléatoires soit
est de calculer les trois
moments du deuxième ordre des deux variables aléatoires soit 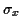 ,
,
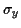 et
et
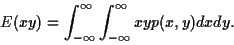 |
(51) |
Si 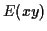 n'est pas nul, alors que
n'est pas nul, alors que 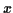 et
et 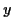 ont une moyenne
nulle, il y a une corrélation entre les deux variables. Cependant
le fait que
ont une moyenne
nulle, il y a une corrélation entre les deux variables. Cependant
le fait que 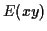 soit nul ne veut pas dire qu'il y a
indépendance entre les deux variables (on parle d'orthogonalité):
l'indépendance suppose la factorisation de la densité de
probabilité du couple sous la forme (51).
En pratique, si on dispose de
soit nul ne veut pas dire qu'il y a
indépendance entre les deux variables (on parle d'orthogonalité):
l'indépendance suppose la factorisation de la densité de
probabilité du couple sous la forme (51).
En pratique, si on dispose de 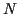 observations
observations 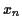 et
et 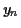 , on
calcule
, on
calcule
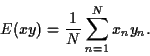 |
(52) |
On définit ainsi le coefficient de corrélation entre 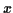 et
et
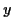 :
:
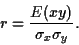 |
(53) |
D'après l'inégalité de Schwarz, le coefficient 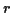 est compris entre
est compris entre 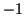 et
et 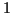 .
Si
.
Si 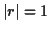 , on peut affirmer qu'il y a une dépendance linéaire
entre
, on peut affirmer qu'il y a une dépendance linéaire
entre 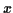 et
et 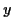 :
:
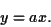 |
(54) |
Plus 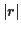 est proche de
est proche de 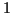 , plus la corrélation est forte. Dans
ce cas les courbes de niveau de la densité de probabilité du couple de variables aléatoires
ont une forme d'ellipse très allongées. Au contraire lorsqu'on a normalisé les variables de sorte que
, plus la corrélation est forte. Dans
ce cas les courbes de niveau de la densité de probabilité du couple de variables aléatoires
ont une forme d'ellipse très allongées. Au contraire lorsqu'on a normalisé les variables de sorte que
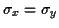 lorsque
lorsque 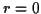 , ces courbes de niveau ont en général (mais pas toujours) une forme
circulaire.
, ces courbes de niveau ont en général (mais pas toujours) une forme
circulaire.
Remarque : affirmer qu'une variable aléatoire est corrélée à une
autre ne permet pas de dire que l'une est la cause de l'autre. On
peut raisonnablement dire que parmi les nombreuses causes qui
influent sur leur comportement il y en a de communes.
On peut définir de la même manière les différents moments du
couple de variables aléatoires ainsi que la fonction
caractéristique bidimensionnelle, qui a un rôle utile dans l'étude
des couples de variables aléatoires.
[ Table des matières ]