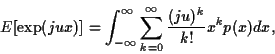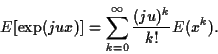Certains développements sont considérablement facilités par le
calcul de la transformée de Fourier de la densité de probabilité.
C'est en particulier le cas lorsqu'on cherche à mettre en
évidence l'indépendance de variables aléatoires. On appelle cette
transformée de Fourier la ``fonction caractéristique'' et on la
note (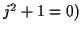
 |
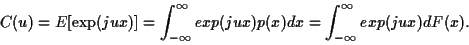(37) |
On notera que cette fonction caractéristique permet d'étudier
aussi bien les variables aléatoires à valeurs discrètes que les variable
aléatoires réelles.
Si la densité de probabilité est une fonction paire (et donc de
moyenne nulle) sa fonction caractéristique est réelle.
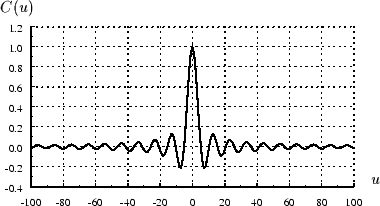
Figure 10:
Fonction caractéristique de la variable équirépartie
 |
Si on effectue un développement en série de Taylor ou de MacLaurin
au voisinage de l'origine de la fonction
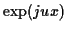, on voit
apparaitre dans le développement de la fonction caractéristique
que le facteur de
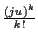est le moment d'ordre 
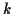de la variable aléatoire
 |
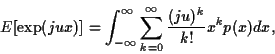(38) |
 |
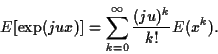(39) |
La fonction caractéristique d'une variable aléatoire gaussienne
s'écrit
 |
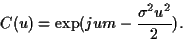(40) |
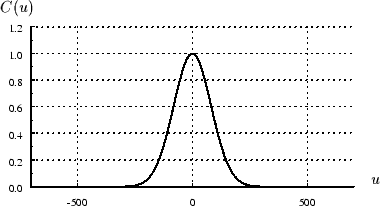
Figure 11:
Fonction caractéristique de la variable gaussienne centrée
 |
Si on multiplie une variable aléatoire par une constante
 |
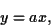(41) |
alors
 |
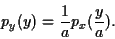(42) |
En en prenant la fonction caractéristique
 |
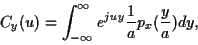(43) |
 |
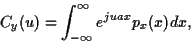(44) |
 |
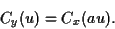(45) |
Ce résultat sera utilisé lors de l'étude de la tendance vers la
loi gaussienne de la somme d'un grand nombre de variables
aléatoires.
En réécrivant cette intégrale en fonction de la variable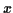 
On peut aussi effectuer le développement du logarithme 
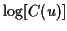de la
fonction caractéristique. On met alors en évidence les
cumulants de la variable aléatoire. Les cumulants d'ordre supérieur à deux sont nuls
lorsque la variable aléatoire est gaussienne, ils jouent un rôle
important dans l'étude des variables aléatoires non gaussiennes,
en particulier pour l'analyse de leur indépendance.
[ Table des matières ]