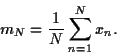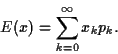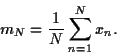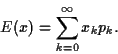Lorsqu'on dispose d'un certain nombre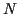 
de résultats 
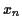pour
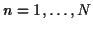, obtenus en répétant plusieurs fois une mesure, il
paraît naturel d'estimer la valeur moyenne du résultat en
calculant
 |
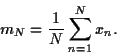(26) |
Si on construit un histogramme de la variable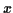 
, le nombre de
fois où le résultat de la mesure appartient à l'intervalle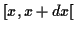 
sera donné par 
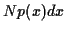. En supposant que 
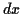est petit, on
peut dans l'expression précédente de la moyenne remplace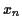r
par 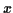lorsque 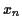est dans l'intervalle 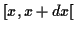. Alors,
quand
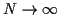
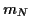tend vers
 |
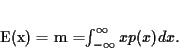(27) |
Lorsque la variable aléatoire est discrète, et prend les valeurs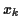 
avec les probabilités 
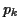, la moyenne est
 |
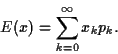(28) |
Si la fonction de répartition de 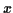présente des discontinuités,
on peut réécrire la formule donnant la moyenne à partir de
l'intégrale (dite de Stiljès) faisant apparaître cette fonction
de répartition et non la densité de probabilité:
 |
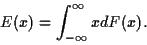(29) |
La première des formules donne la méthode pratique pour calculer
une estimation de la valeur moyenne à partir d'un nombre fini de
mesures tandis que les trois autres donnent des expressions en
fonction des densités de probabilité, expressions nécessaires
pour les développements théoriques.
Lorsqu'on peut calculer ou estimer la valeur moyenne d'une
variable aléatoire, il est souvent judicieux d'en déduire une
nouvelle variable en lui soustrayant cette valeur moyenne de
manière à ne pas alourdir les calculs. Cfette seconde variable est
appelée variable centrée.
Figure 9:
Illustration de la moyenne et de la dispersion d'une variable
aléatoire gaussienne.
Sur chacune des figures, les droites horizontales indiquent la
valeur moyenne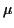 
, la valeur moyenne après soustraction et
addition de l'écart-type, soi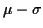t 
et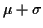 
.
 |
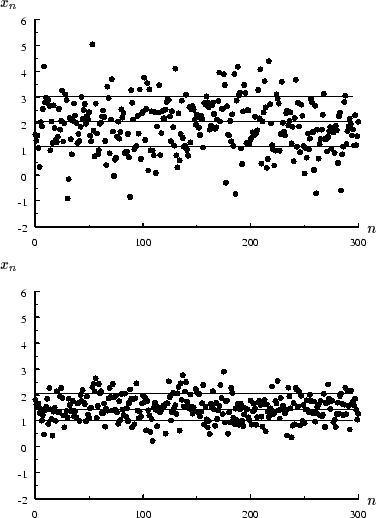La figure 9 montre deux exemples de
variables aléatoires gaussiennes dont les moyennes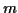 
sont
respectivemen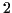t 
et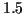 
et les écarts-type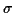 
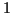et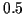 
. Les
marques indiquées sont aux ordonnées 
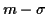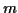, et
.
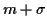[ Table des matières ]