Amplificateur opérationnel

INTRODUCTION.
Comme nous avons pu le constater dans les chapitres précédents, les montages amplificateurs de base à transistors ne sont pas très commodes d'emploi :
ils ne transmettent pas le continu ;
ils sont tributaires des dispersions des transistors, ce qui fait que leurs caractéristiques sont imprécises et non répétables ;
leurs performances sont moyennes, et à moins d'aligner un montage à plusieurs transistors, on ne peut pas avoir simultanément fort gain en tension, haute impédance d'entrée et faible impédance de sortie.
Les amplificateurs opérationnels sont nés au début des années 60, quand on a commencé à intégrer plusieurs transistors et résistances sur le même substrat de silicium ; cette technologie a permis de bâtir des montages complexes, et de les faire tenir sur une petite plaquette de silicium encapsulée dans un boîtier (généralement à 8 broches) commode d'emploi.
Avec ces composants, on a eu accès à des amplificateurs simples d'utilisation, transmettant des signaux continus, et à mise en œuvre facile à l'aide de quelques composants annexes (résistances, condensateurs...) ; les caractéristiques des montages obtenus ne dépendent quasiment plus de l'amplificateur opérationnel, mais uniquement des composants passifs qui l'accompagnent, ce qui garantit une bonne fiabilité du résultat et assure sa répétabilité.
Les amplificateurs opérationnels ont beaucoup progressé depuis leur création, et tendent maintenant à devenir très proches de l'amplificateur idéal (l'amplificateur opérationnel parfait, AOP).
L'AMPLIFICATEUR OPÉRATIONNEL PARFAIT.
1. PRINCIPE.
  A la base, l'AOP est un amplificateur différentiel, donc muni de deux entrées , l'une dite non inverseuse (V₊) et l'autre inverseuse (V_-), et d'une sortie (s) :
  
  Fig. 1. Symbole d'un amplificateur différentiel.
  
  La fonction de transfert complète en continu (en pratique, A_vd et A_vmc dépendent de la fréquence) de cet amplificateur est donnée par la formule :
  
  A_vd est le gain en tension différentiel de l'amplificateur, et A_vmc le gain en tension de mode commun. Dans le cas d'un amplificateur parfait, on fait l'hypothèse que ces gains ne dépendent pas de la fréquence.
  Les gains, ainsi que les impédances d'entrée et de sortie d'un AOP doivent répondre à des critères précis. On peut donner un schéma équivalent de l'AOP :
  
  Fig. 2. Schéma équivalent d'un AOP.
2. CARACTÉRISTIQUES.
  Pour que cet amplificateur soit parfait, les gains en tension doivent répondre aux caractéristiques suivantes :
  A_vd =
  A_vmc = 0
  On distingue deux types d'impédances d'entrée dans un AOP : l'impédance différentielle et celles de mode commun, qui sont définies sur le schéma de la figure 2.
  Un ampli parfait doit répondre aux critères suivants du point de vue des impédances :
  Z_ed =
  Z_emc =
  Z_s = 0
  En résumé : un amplificateur opérationnel parfait est un amplificateur de différence pur à gain différentiel infini, rejetant parfaitement le mode commun, dont les impédances d'entrées sont infinies et l'impédance de sortie est nulle. En pratique, nous verrons que l'amplificateur opérationnel réel présente des défauts par rapport à l'idéalisation que constitue l'AOP, mais le modèle de ce dernier est suffisant pour étudier la plupart des montages simples sans faire des calculs laborieux et inutiles : en effet, du point de vue impédances et gains, et sauf à utiliser les composants à leurs limites, les amplis réels sont suffisamment près des AOP pour qu'on fasse les approximations avec une erreur minime (très souvent mieux que le %). Seul le comportement fréquentiel pose vraiment problème par rapport au modèle idéal.
3. FONCTIONNEMENT D'UN SYSTÈME BOUCLÉ.
  Tous les montages fondamentaux vont être étudiés avec les hypothèses relatives au modèle d'AOP parfait telles que décrites précédemment.
  Dans ces hypothèses, on a vu que le gain en tension différentiel tendait vers l'infini : cela implique que la tension d'entrée différentielle (V₊ - V_-) va devoir tendre vers 0 pour que la tension de sortie soit finie (voir équation [1]).
  Une grande conséquence de ceci est qu'on n'utilisera (quasiment) jamais un amplificateur opérationnel en boucle ouverte pour un fonctionnement linéaire ; on l'utilisera toujours avec une contre réaction, soit en boucle fermée : on réinjectera une fraction de la tension de sortie sur l'entrée inverseuse (retour du signal en opposition de phase). Nous allons maintenant étudier quelques rudiments de la théorie des systèmes bouclés pour mieux comprendre le fonctionnement des montages classiques utilisant des AOP.
  1. Schéma-bloc d'un système bouclé.
    On peut représenter un système bouclé à une entrée et une sortie de la manière suivante :
    
    Fig. 3. Système bouclé.
    Le signal est d'abord atténué en passant dans le bloc de fonction de transfert (qui dans beaucoup de cas est égale à l'unité : on peut alors supprimer ce bloc), et arrive ensuite dans un mélangeur différentiel.
    Dans ce mélangeur, une fraction du signal de sortie est soustraite du signal d'entrée atténué. Le tout est multiplié par la fonction de transfert du bloc A. On obtient l'équation suivante :
    
    On peut en tirer le rapport H=s/e, qui est la fonction de transfert du système bouclé :
    
    Le produit AB est le gain de boucle du système ; dans un système bouclé, on cherche à ce qu'il soit le plus grand possible de manière à ce que H dépende très peu de A. En effet, si AB>>1, on peut écrire :
    
    Si et B sont bien maîtrisés (ce sont la plupart du temps des réseaux constitués de composants passifs de précision correcte), la fonction de transfert H ne dépendra quasiment plus de la fonction de transfert A, qui pourra être assez imprécise, pourvu que sa valeur soit élevée. On réalise un asservissement de la sortie à l'entrée au facteur /B près.
    Deux autres avantages (que nous ne démontrerons pas ici) concernent les impédances d'entrée et de sortie :
    l'impédance différentielle d'entrée est multipliée par le gain de boucle.
    l'impédance de sortie est divisée par le gain de boucle.
    Ces deux propriétés sont importantes, car elles vont permettre d'améliorer les performances apparentes des amplificateurs réels, et donc de justifier encore mieux le fait qu'on utilise le modèle de l'AOP pour faire les calculs.
  2. Application à l'AOP.
    Le fonctionnement en asservissement tel que décrit précédemment va convenir idéalement aux amplificateurs opérationnels : ceux-ci présentent un gain en tension très élevé, mais défini à un facteur trois ou quatre près sur un lot de composants et en fonction des conditions d'utilisation (charge, température...). Le fait de les boucler va permettre de s'affranchir de leurs imperfections.
    L'AOP est un amplificateur différentiel à grand gain. On peut reprendre le schéma de la figure 3 et l'adapter à son cas.
    
    Fig. 4. L'AOP bouclé.
    Ce montage appelle quelques commentaires :
    La fonction de transfert A est le gain différentiel de l'amplificateur (infini pour un AOP, très grand et dépendant de la fréquence pour un ampli réel).
    les blocs et B sont des quadripôles (donc munis de deux entrées et de deux sorties) ; dans le cas des montages à AOP, ces quadripôles ont en fait une entrée et une sortie reliées à la masse : elles ne sont pas représentées sur les schémas blocs.
    si le signal d'entrée e rentre (via le bloc ) sur l'entrée V_-, il faudra rajouter un signe - à pour que les équations précédentes soient vérifiées.
    On a vu que dans le cas de l'AOP, le gain A est infini. Le gain de boucle sera donc lui aussi infini, et à la sortie du mélangeur différentiel, on va avoir un signal qui tend vers 0 pour que le signal de sortie s ait une valeur finie.
    L'amplificateur ne va pas amplifier le signal proprement dit, mais l'écart entre l'entrée et la sortie qui va donc copier fidèlement l'entrée au facteur /B près. On parle alors d'amplificateur d'erreur.
  3. Calcul des montages à AOP.
    Il existe deux alternatives pour calculer les montages à amplificateurs opérationnels : utiliser la loi d'ohm, ou les traiter par la méthode des schémas-blocs.
    Pour la suite du cours, les montages (qui sont des montages de base, donc simples) seront calculés à l'aide de la loi d'ohm ; toutefois, pour illustrer au moins une fois le calcul par schéma-blocs, nous allons traiter l'amplificateur inverseur par cette méthode.
    Pour des montages un peu compliqués, la loi d'Ohm (et ses dérivés : théorème de superposition, Thévenin...) donnent assez vite des mises en équation laborieuses ; de plus, si on veut prendre en ligne de compte le comportement fréquentiel de l'amplificateur réel, les calculs deviennent trop complexes et peu intelligibles.
    On calculera alors les montages par la méthode des blocs. Cette méthode est aussi très pratique dans le cas de calcul de fonctions de transferts à l'aide d'outils informatiques : le problème est bien décomposé et donc plus facile à simuler.
MONTAGES DE BASE À AOP.
Dans "amplificateur opérationnel", il y a deux mots :
amplificateur : c'est la fonction de base de ce composant ; on va étudier plusieurs montages amplificateurs de base.
opérationnel : les caractéristiques de cet ampli nous donnent la possibilité de créer des fonctions mathématiques telles que dérivée, intégrale, Log... Ces fonctions ont autrefois (il y a 25 ans !) été utilisées dans des calculateurs analogiques, et permettaient notamment de résoudre des équations différentielles, et ainsi de simuler des réponses de systèmes physiques divers (mécaniques, acoustiques...). D'où le nom "opérationnel". Nous étudierons les fonctions opérationnelles de base.
1. AMPLIFICATION
  1. Amplificateur inverseur.
    C'est le montage de base à amplificateur opérationnel. L'entrée non inverseuse est reliée à la masse ; le signal d'entrée est relié à l'entrée inverseuse par une résistance R₁, et la sortie est reliée à cette entrée par une résistance R₂.
    
    Fig. 5. Amplificateur inverseur.
    - Calcul par la loi d'ohm.
      La mise en équation est très simple, et s'appuie sur les conditions vues lors de la définition de l'AOP :
      les impédances d'entrée étant infinies, il n'y a pas de courant qui rentre dans l'entrée inverseuse (V_-) ; par conséquent, tout le courant i arrivant dans R₁ ira par R₂ vers la sortie de l'AOP.
      Le gain A_vd est infini ; dans ces conditions, (V₊ - V_-) va tendre vers 0.
      De cette dernière constatation, on peut tirer une équation simplissime, mais fondamentale, et toujours vraie en fonctionnement linéaire :
      
      Comme V₊ est à la masse, V_- se retrouve au même potentiel : comme ce point n'est pas relié physiquement à la masse, on parle de masse virtuelle ; pratiquement, et du point de vue calcul, tout se passe comme si V_- était vraiment relié à la masse.
      Ces constatations étant faites, le calcul du gain en tension est un jeu d'enfant :
      
      On fera attention à l'expression [7] : la tension et le courant sont dans le même sens, d'où le signe -.
      Le gain en tension est donc négatif, et sa valeur ne dépend que des deux résistances R₁ et R₂, qui peuvent être très précises : contrairement aux montages à transistors, le résultat va être fiable et répétable !
      Le calcul de l'impédance d'entrée est aussi simple :
      
      On voit ici les limites de ce montage amplificateur : pour obtenir un fort gain en tension, il faut augmenter R₂ et diminuer R₁ ; or, on va de ce fait diminuer l'impédance d'entrée. Comme celle ci devra rester suffisamment grande et que d'autre part, on ne peut pas augmenter R₂ au delà de quelques M (problèmes de bruit, les imperfections des amplis réels deviennent sensibles...), le gain sera limité et ne pourra pas trop dépasser quelques centaines, ce qui est déjà très bon !
      L'impédance de sortie sera nulle, comme celle de l'AOP, et comme celle de tous les autres montages basés sur un AOP :
    - Calcul par la méthode des schémas-blocs.
      On a ici un réseau de deux résistances partant de l'entrée et aboutissant à la sortie, en passant par l'entrée - de l'ampli.
      Comment se ramener à un schéma équivalent à celui de la figure 4 ? D'abord, on remarque qu'aucun signal n'arrive sur l'entrée + de l'ampli : c'est un des cas où on va mettre un signe - au terme . Ensuite, pour calculer et B, il va falloir utiliser le théorème de superposition.
      Partant de ces deux remarques, on peut définir le quadripôle (figure 6). Il devrait théoriquement arriver sur l'entrée + de l'ampli, on compensera le fait qu'il arrive sur l'entrée - par un signe -. Pour déterminer le quadripôle , on utilise le théorème de superposition : on considère que V_s est égal à 0, seule compte la contribution de V_e. La valeur de est alors triviale (pont diviseur) :
      
      Fig. 6. Quadripôle .
      De la même manière, on va obtenir le quadripôle B : théorème de superposition, on "éteint" la source V_e, et ici, pas de signe -, car B reboucle bien sur l'entrée - de l'ampli.
      
      Fig. 7. Quadripôle B.
      B vaudra :
      
      Au final, si on applique le résultat de l'équation [4] à nos valeurs, on obtient bien :
      
      On note que dans ce cas, la méthode des schémas-blocs est plus longue que l'utilisation de la loi d'ohm : nous l'avons déjà dit, elle devient "rentable" quand le schéma se complique, ou pour faire des simulations sur ordinateur (logiciels de tracé de courbes travaillant en complexes, calculateurs vectoriels et matriciels...)
  2. Généralisation à des dipôles quelconques.
    
    Fig. 8. Amplificateur inverseur généralisé.
    On a précédemment établi un résultat pour deux résistances R₁ et R₂ ; on peut appliquer ce résultat à n'importe quels dipôles d'impédances Z₁ et Z₂. La condition que Z₁ et Z₂ soient des dipôles est fondamentale. Le gain en tension est le suivant :
    
    Ceci ouvre la voie à tout une panoplie de filtres et correcteurs en fréquence divers et variés ; le gros avantage de l'AOP par rapport à des circuits purement passifs, c'est qu'on va pouvoir amplifier le signal à certaines fréquences, et non plus seulement l'atténuer, ce qui offre des débouchés nouveaux et intéressants.
  3. Amplificateur non inverseur.
    L'amplificateur non inverseur est le deuxième amplificateur de base. Pour calculer le gain en tension, on va se servir de l'équation [5] et en déduire :
    
    R₂ et R₁ forment un pont diviseur entre V_s et V_- , soit :
    
    On en tire :
    
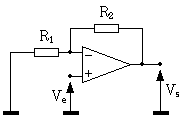
    Fig. 9. Amplificateur non inverseur.
    Le gain est non seulement positif (ampli non inverseur), mais il est aussi toujours supérieur à 1, alors que l'ampli non inverseur autorisait un gain (en valeur absolue) inférieur à 1, soit une atténuation. Notons que pour un ampli, cette caractéristique n'est pas trop gênante...
    Pour ce qui est de l'impédance d'entrée, on attaque directement l'entrée de l'ampli : elle sera donc infinie dans le cas d'un AOP, et très grande dans tous les cas ; de plus, elle ne dépend pas du gain choisi, ce qui laisse plus de latitude dans le choix de R₁ et R₂ pour régler le gain que dans le cas du montage inverseur. L'impédance de sortie est nulle :
    
    On a donc ici un ampli qui présente des caractéristiques idéales ! En pratique, seul le comportement en fréquence de l'amplificateur opérationnel réel viendra ternir le tableau.
    On notera la simplicité de mise en œuvre du montage, comparé à un étage à transistor : impédances idéales, gain ajustable à loisir et de façon précise, voire réglable par un simple potentiomètre, transmission de signaux continus, tout ceci avec un seul amplificateur opérationnel (généralement en boîtier 8 broches) et deux résistances !
    Tout comme pour l'amplificateur inverseur, une généralisation de ce montage est faisable avec n'importe quels dipôles d'impédance Z₁ et Z₂ remplaçant respectivement les résistances R₁ et R₂. l'expression du gain devient :
  4. Montage suiveur.
    Ce montage est une extrapolation de l'ampli précédent, avec R₁ = et R₂ = 0. On obtient un montage tout simple, de gain unité, dont la seule fonction est l'adaptation d'impédance. On le placera donc en tampon entre deux portions de circuit de façon à les isoler l'une de l'autre pour prévenir toute interaction parasite.
    Ce circuit est aussi idéal en entrée et en sortie d'un montage pour bénéficier d'impédance d'entrée infinie (ou presque) et d'impédance de sortie très basse.
    
    Fig. 10. Amplificateur suiveur.
2. MONTAGES OPÉRATIONNELS.
  Après les fonctions d'amplification de base, on va voir plusieurs montages opérationnels, dans le sens où ils vont réaliser des opérations arithmétiques sur un ou plusieurs signaux.
  1. Additionneur inverseur.
    
    Fig. 11. Amplificateur sommateur inverseur.
    On a souvent besoin de mélanger plusieurs signaux ensemble ; la difficulté réside dans le fait qu'il faut éviter toute interaction de réglage des gains affectés aux différentes entrées, ceci pour deux raisons :
    si on doit recalculer tout l'échafaudage à chaque modification du gain d'une entrée, ou en cas de rajout d'une entrée, le montage n'est pas vraiment pratique.
    on ne peut pas faire varier le gain de chaque voie indépendamment des autres, à l'aide d'un potentiomètre, par exemple, alors que c'est une fonction souvent demandée à ce genre de montage.
    Le circuit décrit ici permet de s'affranchir de ces défauts.
    À la base de ce montage, on retrouve l'amplificateur inverseur ; on avait vu que l'entrée inverseuse était considérée comme une masse virtuelle, et qu'aucun courant n'entrait dans l'AOP. De ce fait, chaque courant i_i ne dépend que de la tension d'entrée V_ei et de R_i relatif à sa branche : il n'y aura donc pas d'interaction entre les différentes entrées.
    On a :
    
    La loi des nœuds en V_- nous donne :
    
    En sortie, on a :
    
    Au global, on obtient pour V_s :
    
    On voit qu'on peut ajuster le gain globalement en jouant sur R, et le gain de chaque entrée en jouant sur les résistances R_i. Ce montage offre donc toutes les souplesses.
    On peut obtenir un additionneur inverseur pur en fixant toutes les résistances du montage à la même valeur.
    Aux chapitre des inconvénients, l'impédance d'entrée de chaque voie i est égale à la résistance R_i :
    
    La latitude de réglage citée précédemment baisse donc un peu du fait de cette contrainte, car plus le gain sera élevé, plus l'impédance d'entrée sera faible.
    Comme d'habitude, l'impédance de sortie de ce circuit est voisine de 0.
  2. Montage soustracteur (différentiel).
    Ce montage permet d'amplifier la différence de deux signaux. C'est un montage de base très important en mesures.
    
    Fig. 12. Amplificateur différentiel.
    Pour calculer le gain en tension de cet étage, on va faire appel à la formule du pont diviseur et au théorème de superposition. Le lien va encore être l'équation :
    
    La tension sur l'entrée non inverseuse est :
    
    La formule du pont diviseur est ici appliquée sans approximation, car l'impédance d'entrée de l'AOP est infinie.
    Le calcul de la tension sur l'entrée inverseuse se fait en deux temps, et avec l'aide du théorème de superposition :
    
    Des équations [29], [30] et [31], on tire :
    
    La formule générale de la tension de sortie de ce montage est donc :
    
    Tel quel, ce montage n'est pas un ampli de différence ; il faut imposer des conditions sur les résistances. Si on pose :
    
    en remplaçant k par sa valeur dans [33] et compte tenu de la propriété suivante :
    
    on obtient :
    
    On a bien en sortie la différence des deux signaux d'entrée multipliée par le gain k.
    Si les résistances ne sont pas bien appariées deux à deux dans le rapport de k (condition [34]), le gain ne sera plus purement différentiel ; il va apparaître un terme de mode commun. Ce défaut sera expliqué en détail dans le cours d'électronique 2 (Amplificateur d'instrumentation).
    Les impédances d'entrée Z_e1 et Z_e2 sont difficiles à cerner, surtout celle de l'entrée inverseuse Z_e2 ; on retiendra qu'elles sont différentes, ce qui peut poser des problèmes pour certaines applications.
    On peut aussi définir une impédance d'entrée différentielle Z_ed et une de mode commun Z_emc. Une de ces impédances est constante, c'est l'impédance d'entrée différentielle Z_ed :
    
    Cette valeur est équivalente à ce qu'on obtient avec l'amplificateur inverseur : elle est faible quand le gain devient élevé.
  3. Montage intégrateur.
    Nous attaquons ici les montages opérationnels plus sophistiqués que de simples additions ou soustractions.
    
    Fig. 13. Montage intégrateur.
    Le calcul de la réponse V_s à un signal d'entrée V_e se traite comme dans le cas de l'amplificateur inverseur. On a :
    
    En sortie, le condensateur a aux bornes de ses armatures une charge électrique q égale à :
    
    Cette charge électrique est l'intégrale du courant i qui traverse le condensateur ; compte tenu du sens de i, on a :
    
    Si on remplace dans [40] i et q par leur valeur en fonction de V_e et de V_s (équations [38] et [39]), on obtient :
    
    On retrouve en sortie l'intégrale du signal d'entrée. Ce montage est délicat à utiliser et devra faire l'objet de précautions : en effet, la moindre tension continue présente à l'entrée (y compris et surtout une tension parasite) sera intégrée et générera une rampe en sortie. Il faudra donc prévoir des dispositifs annexes, soit un système de stabilisation, soit un système de remise à zéro de la sortie.
  4. Montage dérivateur.
    Ce montage est similaire au précédent et se traite de la même manière.
    
    Fig. 14. Montage dérivateur.
    En entrée et en sortie, on a :
    
    Le courant i est la dérivée de la charge électrique q présente sur les électrodes du condensateur :
    
    Au final, on obtient :
    
    La sortie est proportionnelle à la dérivée de l'entrée. Comme pour le montage précédent, avec un amplificateur réel, on aura des difficultés à faire fonctionner ce circuit tel quel (système instable), et il faudra rajouter des éléments pour le rendre pleinement fonctionnel.
  5. Montage logarithmique.
    Dans ce montage, on retrouve la structure traditionnelle de l'ampli inverseur, mais avec une diode en contre-réaction. Cette diode, dont la caractéristique courant/tension est logarithmique va nous donner une fonction de transfert de ce type. En entrée, on a :
    
    Et en sortie :
    
    Lorsque le terme en exponentielle est significativement supérieur à 1 (V_d > 50mV environ), on peut écrire :
    
    Soit, en remplaçant i par sa valeur :
    
    Fig. 15. Montage logarithmique.
    En sortie, on trouve bien une fonction logarithmique du signal d'entrée. Tel quel, ce montage aurait peu d'intérêt ; mais, si on se rappelle qu'additionner des logarithmes revient à faire une multiplication, on en perçoit l'utilité !
    En pratique, et une fois de plus, ce montage (bien que fonctionnel) n'est pas utilisé tel quel : d'abord, il ne fonctionne que pour des tensions d'entrée positives, et il nécessite de sérieuses compensations thermiques pour permettre des opérations précises. De plus, on remplace souvent la diode par une jonction base-émetteur de transistor, linéaire sur une plus grande plage de courant.
  6. Montage exponentiel.
    Pour multiplier deux signaux, il ne suffit pas de prendre le Log de chacun des signaux, et d'additionner ; il faut ensuite prendre l'exponentielle du résultat. Ce circuit est fait pour ça.
    
    Fig. 16. Montage exponentiel.
    Par des calculs analogues aux précédents, on démontre facilement et de la même manière :
    
    En pratique, on trouve des circuits intégrés tout faits comprenant le montage Log, le montage exponentiel, ainsi que les compensations thermiques et diverses possibilités de réglage de gain. Ces montages sont des multiplieurs analogiques, et servent notamment, en mesures, à linéariser certains capteurs. A noter que ces composants sont délicats, coûteux, et présentent des dérives importantes. L'utilité de tels montages est devenue douteuse avec l'introduction massive du traitement numérique.
3. FILTRAGE.
  L'amplificateur opérationnel ouvre les portes d'une kyrielle de fonctions de filtrage, qu'on dénomme filtres actifs, par opposition aux filtres passifs (fabriqués avec des composants du même nom) qui ne peuvent qu'atténuer le signal. Avec un AOP, on va pouvoir amplifier certaines fréquences autant qu'en atténuer d'autres.
  Il est hors de question d'aborder ici tous les filtres possibles (exercice qui n'a de limite que la créativité humaine !) : le lecteur désireux d'approfondir le sujet pourra consulter des ouvrages spécialisés dans le filtrage, et aussi les data books des fabricants d'amplificateurs, qui sont bien souvent une mine d'idées gratuites (qu'on retrouve d'ailleurs souvent telles quelles dans des livres chers...).
  Les filtres classiques d'ordre 1 présentent peu d'intérêt en filtrage actif, l'apport étant faible (au mieux, adaptation d'impédance) par rapport au filtrage passif.
  Nous allons voir deux filtres du deuxième ordre dont la fonction de transfert présente des racines imaginaires ; ceci n'est possible en filtrage passif que si on fait appel à des inductances, qui sont des composants encombrants, rares, imprécis et coûteux. Grâce à l'AOP, on va faire de tels filtres uniquement avec des résistances et des condensateurs.
  1. Passe bas 2e ordre.
    
    Fig. 17. Filtre passe bas du deuxième ordre.
    On peut remarquer qu'à la base, la structure ressemble fort à deux filtres passifs R-C passe bas concaténés. La différence vient du fait que le premier condensateur n'est pas relié à la masse, mais à la sortie du filtre qui est isolée de la deuxième cellule passe-bas par un montage suiveur.
    La réponse en fréquence de ce montage est du type :
    
    La fonction de transfert "générique" d'un filtre passe bas d'ordre 2 est du type :
    
    On identifie les deux formules pour les valeurs suivantes de o et z :
    
    Le réseau de courbes de réponse en fréquence (amplitude et phase) de ce filtre est donné en annexe 1 en fonction du coefficient de surtension z.
  2. Passe haut 2e ordre.
    
    Fig. 18. Filtre passe haut du deuxième ordre.
    La topologie de ce filtre est la même que celle du précédent, sauf qu'on a permuté les résistances et les condensateurs. La fonction de transfert est :
    
    La pulsation de cassure et le coefficient de surtension de ce filtre sont :
    
    La réponse en fréquence (amplitude et phase) de ce filtre est donnée en annexe 2.
    Il est possible de concaténer les deux filtres précédents, et de les combiner avec des filtres du premier ordre pour obtenir un filtre d'ordre plus élevé. Des ouvrages traitant des filtres donnent les valeurs des fréquences de cassure et coefficients de surtension adéquats pour obtenir la réponse en fréquence désirée.
4. MONTAGES NON LINÉAIRES.
  Les montages précédents sont qualifiés de "linéaires" car l'amplificateur fonctionne avec la condition V₊ = V_- , soit dans sa plage de fonctionnement en amplificateur linéaire. Il convient de noter que certains des montages étudiés (ex : montage logarithmique) ne sont pas linéaires ! Mais, l'amplificateur, lui, fonctionne en mode linéaire.
  Nous allons voir maintenant plusieurs montages (et il en existe bien d'autres) dans lesquels cette condition n'est plus vérifiée.
  Pour ce faire, on va forcer artificiellement les deux entrées à des valeurs différentes, ce qui impliquera en sortie, du fait du gain infini (très grand pour les amplis réels), que l'ampli ne pourra prendre que deux valeurs : V_sat+ et V_sat-, qui sont respectivement les tensions de saturation positive et négative de l'ampli. En effet , ce dernier est alimenté par deux sources de tension dont on ne pourra pas dépasser la valeurs en sortie.
  Vu que l'ampli ne peut prendre que les deux valeurs des tension en sortie, ces montages sont appelés montages en commutation, et peuvent être interfacés avec des circuits logiques, qui ne connaissent, eux aussi, que deux états.
  1. Comparateur de tensions.
    C'est un montage qui sert de base à de nombreux autres schémas plus élaborés.
    Le principe est simple : on compare un signal d'entrée à une tension de référence, et selon que la valeur du signal est supérieure ou inférieure à la référence, l'ampli prendra l'une ou l'autre des valeurs V_sat+ ou V_sat- en sortie.
    Il existe deux configurations : le comparateur non inverseur (signal sur l'entrée +) et le comparateur inverseur (signal sur l'entrée -). Dans le premier cas, si la référence est égale à 0, la sortie vaut V_sat+ quand le signal est positif et V_sat- sinon. Dans le deuxième cas, on a l'inverse.
    
    Fig. 19. Comparateur non inverseur.
    Si on met un signal sinusoïdal à l'entrée, les chronogrammes d'entrée et de sortie sont :
    
    Fig. 20. Comparateur : chronogrammes
    Important : ce montage est souvent fait avec des amplificateurs opérationnels, mais on remplacera avantageusement ce composant par un comparateur différentiel, qui est une sorte d'amplificateur à grand gain et deux entrées aussi, mais qui est prévu pour fonctionner en mode non linéaire (commutation) de façon bien plus rapide qu'un ampli op qui n'a pas des caractéristiques exceptionnelles dans ce domaine. De plus, ces composants sont souvent conçus pour fonctionner avec une seule alimentation 0-5V de manière à s'interfacer facilement avec des composants logiques.
  2. Trigger.
    Ce montage est très utilisé dans tout système de mesure où l'on doit détecter un seuil : il est donc fondamental.
    Il est une évolution du comparateur, destinée à améliorer les performances avec des signaux bruités.
    Il existe plusieurs schémas possibles. Le montage suivant a été choisi comme cas d'école :
    
    Fig. 21. Trigger.
    A première vue, ce montage ressemble à un ampli inverseur, mais, il ne faut pas se tromper : le réseau de résistances R₁, R₂ est relié à l'entrée +, ce qui fait que cette fois, le signal de sortie revient en phase sur l'entrée ; on a non plus une contre réaction, mais une réaction positive (effet boule de neige), ce qui entraîne la divergence de la tension de sortie vers une des valeurs V_sat+ ou V_sat- .
    Dans ce montage (et les autres montages non linéaires), l'amplificateur fonctionne en comparateur : comme le gain est infini (ou très grand), on a les relations :
    
    Ici, la valeur de V_- est triviale :
    
    Et la valeur de V₊ se calcule aisément à l'aide du théorème de superposition :
    
    Le basculement de la sortie de l'ampli se fait pour V₊ = V_- :
    
    Dans cette formule, il faut garder à l'esprit que V_s ne peut prendre que les deux valeurs V_sat+ et V_sat- .
    Dans le cas particulier où V_ref = 0 et V_sat+ = |V_sat-| = V_sat, on aura :
    
    La figure 22 donne les signaux d'entrée, de sortie, et de l'entrée + de l'amplificateur, pour R₁=10k et R₂=33k :
    
    Fig. 22. Signaux sur le trigger
    En fait, tout se passe comme si on avait un comparateur de tension ayant deux seuils de basculement liés aux états de la sortie : quand la sortie est à l'état bas, le seuil a une valeur haute ; passé ce seuil, la sortie bascule à l'état haut, et le seuil prend une valeur basse. De ce fait, pour faire rebasculer la sortie à l'état bas, il faut que le signal diminue d'une quantité supérieure à la valeur l'ayant faite basculer précédemment : c'est l'hystérésis du trigger.
    Un trigger est caractérisé par son cycle d'hystérésis (la réponse est différente suivant la valeur de l'état de la sortie).
    Le cycle relatif aux signaux de la figure 22 (mêmes valeurs de composants) est le suivant :
    
    Fig. 23. Cycle d'hystérésis du trigger
    Ce cycle est centré autour de zéro, qui est la valeur de la tension de référence V_ref. On y voit les deux seuils de basculement de la sortie ; La différence de ces deux seuils est la valeur de l'hystérésis.
    Ce cycle est ici symétrique pour deux raisons :
    V_ref = 0
    V_sat+ = |V_sat-| = V_sat
    Si on modifie ces valeurs, le cycle va devenir asymétrique par rapport à la tension de référence.
    Quelle est l'utilité d'un tel montage ? Lorsqu'on doit transformer un signal analogique en signal numérique binaire (deux états définis par une valeur de seuil sur le signal analogique), si le signal d'entrée varie très lentement et/ou est bruité, on peut avoir un phénomène oscillatoire en sortie de l'amplificateur dû au bruit ou à des réactions parasites de la sortie sur l'entrée. Pour prévenir ces oscillations, on "verrouille" le signal de sortie en en réinjectant une partie sur l'entrée +. Pour qu'il y ait des oscillations parasites, il faut que la tension d'entrée varie de l'opposé de la valeur de l'hystérésis juste après le basculement. Cette dernière est ainsi ajustée en fonction du bruit présent sur le signal d'entrée.
    Comme pour le montage comparateur vu précédemment, un comparateur différentiel remplacera avantageusement l'amplificateur opérationnel.
  3. Multivibrateur astable.
    Le but de ce montage est de délivrer un signal carré en sortie : c'est un générateur de signal autonome.
    
    Fig. 24. Multivibrateur astable.
    Sur le schéma, on peut distinguer un trigger légèrement différent de celui de la figure 21 : l'entrée se fait sur l'entrée - de l'ampli ; l'hystérésis se fait là aussi par un réseau de résistances en réaction positive sur l'entrée +, une des extrémités de R₁ étant reliée à la tension de référence (ici, la masse).
    L'entrée est connectée ici à un circuit R-C alimenté par la sortie de l'amplificateur.
    Un oscillogramme est donné en figure 25, qui permet de mieux comprendre le fonctionnement de ce montage.
    
    Fig. 25. Signaux sur un multivibrateur
    Nous ferons l'hypothèse que V_sat+ = |V_sat-| = V_sat.
    Supposons qu'à la mise sous tension, le condensateur soit déchargé, et que V_s=+V_sat. La tension aux bornes de V₊ est donnée par la relation suivante (elle est positive) :
    
    La sortie alimente un circuit R-C, et C se charge selon la loi exponentielle suivante :
    
    Lorsque V_- = V₊, le trigger bascule (voir figure 25), et on applique alors une tension -V_sat sur le R-C qui devra se décharger de la valeur de l'hystérésis du trigger avant que la sortie ne bascule à nouveau, et ainsi de suite.
    Avec les hypothèses précédentes (V_sat+ = |V_sat-| = V_sat), on aura en sortie du multivibrateur un signal carré (rapport cyclique égal à 0.5), de fréquence égale à :
    
    En pratique, le signal aura un rapport cyclique différent de 1/2 car les tensions de saturation de l'ampli ne sont pas égales, et varient avec la température, la charge...
    Pour obtenir un signal "carré" convenable, on utilisera un ampli à fort slew rate, ou beaucoup mieux, comme pour le trigger, un comparateur différentiel.
    Ce type de montage est important du point de vue principe, mais en pratique, il existe des solutions beaucoup plus "propres" pour générer un signal carré. On n'utilisera donc ce montage qu'à titre de dépannage !
  4. Redresseur sans seuil.
    
    Fig. 26. Redresseur sans seuil.
    On a vu dans le cours sur les diodes que le gros problème de ce composant, pour redresser des faibles tensions, provient de son seuil élevé (>0.5V pour le silicium), qui dépend en plus de la température. Cette caractéristique interdit le redressement de faibles signaux avec une précision décente. L'amplificateur opérationnel va nous aider !
    Le montage est celui de la figure 26 : le montage ressemble à un suiveur auquel on a adjoint une diode en série avec l'amplificateur.
    Pour des tensions d'entrée négatives, la sortie de l'ampli va avoir tendance à devenir négative, mais, elle est bloquée par la diode : il n'y a pas de contre-réaction, car le signal de sortie de l'ampli ne peut pas revenir sur l'entrée -. Dans ce cas, la tension de sortie de l'amplificateur va prendre la valeur V_sat-, et la tension de sortie du montage va être nulle.
    Lorsque la tension d'entrée va devenir positive, la sortie de l'amplificateur va devenir positive aussi, et elle va augmenter jusqu'à la valeur de la tension de seuil de la diode, et la contre réaction sur l'entrée - va pouvoir se faire, la tension en sortie de l'ampli prenant la valeur V_d + V_e, de manière à ce que V₊ soit égal à V_- (donc à V_s).
    En bilan, pour des tensions positives, V_s = V_e , et pour des tensions négatives, V_s = 0 : on a un redresseur idéal.
  5. Détecteur de crête.
    
    Fig. 27. Détecteur de crête.
    Pour conserver la valeur crête d'une tension, on peut commencer par redresser celle-ci, et en adjoignant un condensateur au montage redresseur précédent, il est possible de garder en mémoire la valeur de crête.
    Le fonctionnement est le même que pour le redresseur sans seuil, sauf que le condensateur va se charger, et quand la tension d'entrée va diminuer, le condensateur va conserver sa charge (à condition que l'entrée - de l'ampli soit à très haute impédance et que la charge de sortie ait aussi une très haute impédance -montage suiveur par exemple), et la diode va se bloquer, car la tension de sortie va diminuer jusqu'à la valeur -V_sat (plus de contre réaction à cause de la diode).
    Il faut prévoir un dispositif annexe pour décharger le condensateur afin de faire une nouvelle mesure : sur le schéma, on a placé un simple transistor de façon schématique, mais celui-ci pourra être remplacé avantageusement par un commutateur analogique à base de FET ou de MOS.
    NB : dans ce montage, on peut remplacer la diode par un commutateur analogique bi-directionnel commandable en tension. On va alors pouvoir bloquer le signal à l'instant désiré et le conserver ; c'est le principe de base de l'échantillonneur-bloqueur (voir cours d'électronique 2).
L'AMPLIFICATEUR OPÉRATIONNEL RÉEL.
Avant d'attaquer tous les défauts de l'amplificateur réel, et afin de mieux les comprendre, nous allons étudier un schéma de principe de cet amplificateur.
Ce schéma n'est évidemment pas un schéma réel, mais il contient tous les ingrédients fondamentaux d'un amplificateur ; c'est cette architecture qui est aussi utilisée dans des montages de puissance (amplificateurs HIFI et industriels), et donc, la compréhension de cette architecture est importante et permettra d'investiguer des domaines autres que celui de l'amplificateur opérationnel.
1. SCHÉMA INTERNE DE PRINCIPE.
  Sur le schéma de la figure 28, nous avons représenté les deux alimentations V_al+ (positive) et V_al- (négative), les deux entrées V₊ et V_-, et la sortie V_s de l'amplificateur.
  L'ampli est constitué de trois étages :
  un étage d'entrée différentiel (T₁ et T₂), avec sa charge d'émetteurs (source de courant I₁) et ses charges de collecteurs (miroir de courant T₃ et T₄).
  un étage de gain formé de T₅ et de sa charge active I₂.
  Un étage de sortie push pull constitué par les transistors T₆ et T₇ polarisés par les diodes D₁ et D₂.
  
  Fig. 28. Schéma de principe d'un amplificateur.
  - Étage différentiel :
    On a représenté ici un étage différentiel classique : deux transistors montés dans une configuration de type émetteur commun (entrée sur la base, sortie sur le collecteur) avec les deux émetteurs reliés à une source de courant. Cette source I₁ doit être la plus proche possible de l'idéal, car la valeur de sa résistance interne détermine le taux de réjection du mode commun.
    Les charges de collecteur ne sont pas des résistances, mais des charges actives, constituées des transistors T₃ et T₄ montés en miroir de courant : le transistor T₃ est utilisé en diode (le collecteur est relié à la base), et détermine le potentiel de base de T₄, donc son courant de collecteur. Sur le circuit intégré, on peut construire T₃ et T₄ de manière à ce qu'ils aient les mêmes caractéristiques de gain, V_be... (idem pour T₁ et T₂) : le courant dans la branche T₁/T₃ sera le même que celui de la branche T₂/T₄.
    On démontre que le miroir de courant est une astuce permettant de doubler le gain de l'étage différentiel.
    La sortie de cet étage se fait sur le collecteur de T₂, et c'est la résistance dynamique de T₄ (le 1/h₂₂) qui charge T₂. Le gain sera donc plus élevé que si on avait une simple résistance à la place de T₄.
    Le gain de cet étage est de l'ordre de 100.
    L'impédance d'entrée différentielle de ce montage est égale à 2h₁₁ (le h₁₁ de T₁ ou de T₂). Pour que cette impédance soit grande (1M pour un µA741), il faut que le courant de polarisation de base soit très faible (quelque dizaines de nA).
    Les amplificateurs plus récents font en général appel à des transistors FET en entrée (LF356 de NS, TL081 de Texas...) voire MOS (LMC660). La structure de l'étage reste similaire.
    En pratique, les montages sont un peu plus compliqués, et les transistors T₁ et T₂ sont souvent remplacés par 4 transistors, deux collecteurs communs qui attaquent deux bases communes. C'est une astuce technologique permettant d'améliorer la plage d'entrée différentielle de l'ampli.
  - L'étage de gain :
    Le deuxième étage est très simple, c'est un montage émetteur commun constitué de T₅, chargé par une source de courant (en général, c'est encore un montage à miroir de courant) : la charge dynamique de T₅ est donc la résistance parallèle de la source de courant I₂ ; le gain est très élevé (environ 1000, ce qui fait un ordre de grandeur de 10⁵ pour l'ensemble !).
    On note la capacité C entre base et collecteur du transistor T₅ : c'est une capacité destinée à la compensation de l'amplificateur ; la fréquence de cassure de ce filtre est très basse (quelques dizaines d'hertz) et permet à la plupart des amplis d'être inconditionnellement stables. Cette capacité utilise l'effet miller : le filtre est constitué de l'impédance de sortie du premier étage (très élevée) et de la capacité C, le tout multipliée par le gain en tension du deuxième étage. On peut obtenir une fréquence de cassure très faible avec une capacité très petite (quelques dizaines de pF), qui peut ainsi être intégrée sur la puce.
  - L'étage de sortie :
    C'est un étage push pull constitué de deux transistors complémentaires qui fonctionnent en collecteur commun, T₇ pour les alternances positives, et T₈ pour les alternances négatives. Ces transistors sont polarisés par les deux diodes D₁ et D₂ afin de limiter la distorsion de croisement.
    Du point de vue petits signaux, cet étage de sortie (et sa charge, qui est déterminée par l'utilisation que l'on fait de l'ampli, et donc, va varier) vient se mettre en parallèle sur la charge de collecteur de T₅ : le gain de l'étage intermédiaire va ainsi dépendre de la charge qu'on connectera en sortie de l'ampli.
    Dans les amplis réels, l'étage de sortie est plus complexe, et comprend notamment des étages de protection contre les courts-circuits, qui vont limiter le courant de sortie de l'ampli à des valeurs raisonnables.
2. ALIMENTATION.
  Comme pour tout composant dit "actif", notre amplificateur ne va pas sortir du néant l'énergie qu'il fournit à l'extérieur. Il va falloir l'alimenter afin de polariser tous les transistors qui le composent.
  Sur le schéma de la figure 28, on voit deux entrées d'alimentation, V_al+ et V_al-. On remarque que nulle part sur ce schéma, la masse n'est présente ! En pratique, les deux alimentations sont référencées à la masse, et ce sont les tensions d'entrée qui vont fixer tous les potentiels par rapport à la masse, du fait de la contre réaction (la tension de sortie est liée aux tensions d'entrée qui sont liées à la masse).
  Cette caractéristique est intéressante, et va nous permettre d'alimenter l'amplificateur opérationnel de deux manières différentes :
  symétrique : on alimente l'ampli par deux sources égales et opposées. Tout l'ampli est ainsi polarisé symétriquement par rapport à la masse. C'est le mode d'alimentation le plus courant. Il faut noter que les deux tensions peuvent être inégales : le fonctionnement de l'ampli ne sera pas affecté, mais la plage de sortie sera limitée par l'alimentation la plus faible (signaux symétriques par rapport à la masse).
  unipolaire : V_al+ est relié à une alimentation positive et V_al- est relié à la masse. Ce système est pratique pour un fonctionnement sur piles ou batteries, mais il faudra alors polariser les signaux d'entrée à une valeur convenable pour que l'ampli fonctionne correctement (il n'y a pas de miracles, c'est un système à transistors qui nécessite une polarisation !). Ce mode de fonctionnement interdit l'amplification de signaux continus.
  Les tensions d'alimentation des amplificateurs opérationnels courants peuvent varier dans une large gamme, typiquement de ±2.5V à ±5V mini jusqu'à ±18V à ±22V maxi.
  Certains amplis sont spécialisés dans les basses tensions (alimentation par pile) et d'autres dans des tensions plus élevées. Pour des applications particulières, on consultera l'abondante documentation fournie par les constructeurs.
  Certains amplificateurs rapides nécessitent un découplage soigné des alimentations : on mettra un condensateur de découplage (typiquement 10 à 100nF céramique) entre chaque borne d'alimentation et la masse, ceci aux plus près des broches d'alimentation. Sans ces précautions, on pourra avoir des montages présentant des fonctionnements erratiques, voire des oscillations parasites aboutissant à la destruction de l'ampli (cas du LM318 !).
  Outre la plage de tensions d'alimentation, les amplificateurs sont caractérisés par leur courant de consommation : il faut alimenter tous les composants internes pour les polariser. Le courant de polarisation va être plus ou moins important selon la conception de l'ampli, et le compromis recherché : il existe des amplis à très faible courant de consommation, destinés principalement aux applications fonctionnant sur piles et batteries ; en corollaire, leurs performances en fréquence seront médiocres (voir cours sur les transistors : plus la polarisation est faible, plus les impédances mises en jeu sont grandes, et plus les capacités parasites des transistors prennent de l'importance, dégradant le comportement à haute fréquence). A côté de ces amplis, il en existe d'autres à courant de consommation élevé, ayant des bonnes performances en haute fréquence.
  Certains amplificateurs, dits "programmables" ont une possibilité de réglage du courant de polarisation (et donc du compromis consommation/rapidité), et peuvent ainsi s'adapter au besoin de l'utilisateur.
  Exemples de courants de consommation :
  LM4250 : réglable de 1 à 250µA
  LF441 : 200µA
  µA741 : 2mA
  LM318 : 5mA
  Ces amplis sont donnés du plus lent au plus rapide : produit gain-bande passante de 10 à 300kHz pour le LM4250, 1MHz pour le 741, et 15MHz pour le LM318.
3. CARACTÉRISTIQUES D'ENTRÉE.
  1. Impédances d'entrée.
    On a vu que l'amplificateur différentiel présentait deux impédances d'entrée différentes : l'impédance différentielle, relative à la différence de tension entre les deux entrées, et l'impédance de mode commun. On va s'aider du schéma de la figure 28 pour interpréter ces deux impédances.
    - Impédance différentielle.
      Sur le schéma de la figure 28, l'impédance différentielle correspond à 2h₁₁ et dépend directement du courant de polarisation choisi.
      En pratique, cette valeur sera comprise entre quelque centaines de k et quelques dizaines de M pour les amplis à transistors d'entrée bipolaires.
      Les amplis à transistors d'entrée JFET présenteront des impédances beaucoup plus élevées, couramment de l'ordre de 10¹².
      Il existe aussi des amplis en technologie MOSFET qui ont des impédances supérieurs à 10¹⁵ : nous ne sommes vraiment pas loin de l'infini de l'AOP !
      Il convient de noter que la tension d'entrée différentielle sera toujours voisine de zéro (en fonctionnement linéaire) : le courant différentiel consommé sera donc extrêmement faible, même si les résistances connectées à l'ampli ont des valeurs voisines de l'impédance d'entrée de celui-ci. On pourra donc dans la majorité des cas négliger l'impédance d'entrée dans les calculs.
    - Impédance de mode commun.
      On peut voir cette impédance comme celle de deux montages collecteur commun en parallèle dont la charge commune d'émetteur est une source de courant de résistance dynamique très élevée. Vue de l'entrée, cette résistance est multipliée par le gain des transistors : elle sera très élevée dans tous les cas, et donc négligée dans les calculs.
  2. Tension de décalage d'entrée (offset).
    C'est un des principaux défauts de l'amplificateur réel, et pour des forts gains en tension et/ou des faibles tensions d'entrée, on devra en tenir compte.
    Cette tension est due au fait que les transistors d'entrée ne sont pas rigoureusement identiques (T₁ et T₂ sur la figure 28), et que pour obtenir une tension nulle en sortie, il faudra appliquer une tension différentielle non nulle à l'entrée, cette tension étant l'écart de V_be de T₁ et T₂ à courant de collecteur donné.
    Quand on modélise un montage à amplificateur opérationnel avec une erreur d'offset, on le représente en général par le schéma suivant :
    
    Fig. 29. Erreur d'offset.
    Cette représentation n'est pas forcément judicieuse, car on peut obtenir des courants parasites dûs à cette source dans les composants d'entrée, alors qu'en fait, l'écart de courant ne peut venir que de la sortie qui compense la tension de décalage ; en effet, on aura la relation :
    
    Avec une telle relation, quand l'ampli fonctionne en mode linéaire, on n'a plus V₊ = V_-, mais V₊ = V_-+V_d. A noter que V_d est une valeur algébrique, et peut être positive ou négative.
    Pour les montages en commutation (comparateurs et triggers entre autres), le seuil de basculement sera lui aussi défini par la relation V₊ = V_-+V_d.
    Ordres de grandeur : V_d va valoir de quelques dizaines de µV pour des amplis de mesure (OP27 : 25µV) à une dizaine de mV pour des amplis à entrée JFET standards (TL081 par exemple).
  3. Courants de polarisation.
    Sur le schéma de la figure 28, on remarque qu'il n'y a aucun circuit de polarisation des bases des transistors d'entrée T₁ et T₂. Par conséquent, cette polarisation devra être assurée par les composants externes du montage à amplificateur.
    Si on reprend l'exemple du montage amplificateur inverseur de la figure 5, la polarisation des bases se fera directement par la masse pour l'entrée +, et par la masse et la sortie de l'ampli via R₁ et R₂ pour l'entrée -. Le courant de polarisation de la base de T₁ va donc circuler dans ces deux résistances, en y créant au passage des chutes de tension parasites.
    
    Fig. 30. Ce qu'il ne faut pas faire !!!
    Une remarque importante qui découle de ceci est qu'il faut toujours laisser le passage du courant continu vers les deux entrées de l'ampli ; il est hors de question de couper ce chemin par un ou plusieurs condensateurs : le montage ne serait alors plus fonctionnel.
    Dans l'exemple de la figure 30, on coupe le chemin de la polarisation de l'entrée + ; T₂ (cf figure 28) ne peut pas être polarisé, et l'ampli ne fonctionne plus.
    Si on voulait vraiment mettre un condensateur en série avec le signal d'entrée pour bloquer sa composante continue, il faudrait rajouter une résistance entre l'entrée + et la masse, de manière à laisser passer le courant de polarisation.
    Ordre de grandeur des courants de polarisation :
    de 30à 500nA pour un µA741, les fortes valeurs étant obtenues à chaud.
    de 3 à 20nA pour un LM627 (ampli rapide de précision)
    de 30pA à 50nA pour un LF356 (entrées JFET) : le courant devient important à chaud !
    Le courant de polarisation peut être rentrant ou sortant, selon le type de transistors utilisés en entrée (NPN ou PNP).
  4. Courants de décalage.
    Le courant de décalage est le pendant de la tension d'offset pour les courants de polarisation : comme les transistors d'entrée sont dissymétriques, les courants de base seront aussi différents. Le courant de décalage est égal à :
    
    Ce courant, en circulant dans les résistances connectées à l'ampli va créer une chute de tension parasite qui va s'ajouter à la tension d'offset.
    Les ordres de grandeurs de ces courants sont d'environ 1/20e à 1/5e de la valeur des courants de polarisation.
  5. Plages de tensions d'entrée.
    On a déjà largement abordé les problèmes de polarisation des amplificateurs, et la figure 28 montre le principe des montages utilisés.
    Sur cette figure, on voit qu'il ne faudra pas dépasser certaines limites pour les tensions d'entrée sous peine de dégrader le fonctionnement, voire de détruire l'amplificateur.
    En pratique, les constructeurs donnent des plages de tension à respecter :
    absolues pour chaque entrée : elles dépasseront rarement les valeurs des tensions d'alimentation. Les entrées sont souvent reliées aux tensions d'alimentation par des diodes connectées en inverse pour le fonctionnement normal, et qui deviennent passantes quand les tensions d'entrée dépassent les valeurs des tensions d'alimentation ; le courant est limité par les résistances câblées en série avec les entrées. Si on applique directement un signal trop élevé sur une des entrées (cas de l'ampli non inverseur), on détruit le composant.
    différentielles : ces valeurs peuvent être faibles (±0.7V, soit la valeur d'un V_be , dans le cas ou on bride les deux entrées avec deux diodes connectées tête bêche).
    de mode commun (souvent les tensions d'alimentation moins quelques volts). Au delà des limites de mode commun admises, la polarisation des étages d'entrée ne se fait plus correctement.
    En bref, il ne faut pas faire n'importe quoi avec un amplificateur opérationnel, et si on a des cas de fonctionnement limites, il faudra s'assurer qu'ils sont autorisés par l'ampli choisi. Tout est ici affaire de compromis, et il existe une grande variété d'amplis sur le marché autorisant certains modes de fonctionnement au détriment d'autres : il faut choisir le bon composant en fonction du problème. Une seule chose est sûre : on n'aura jamais tout en même temps !
4. CARACTÉRISTIQUE DE TRANSFERT.
  La caractéristique de transfert est linéaire : la sortie est proportionnelle à la différence des tensions d'entrée ; il ne faut pas non plus oublier le terme de mode commun (voir équation [1]).
  La tension de sortie est bien évidemment limitée aux deux extrémités de la plage de fonctionnement à V_sat+ et V_sat-.
5. CARACTÉRISTIQUES DE SORTIE.
  1. Impédance de sortie.
    En pratique, l'impédance de sortie des amplificateurs réels n'est pas nulle ; elle reste néanmoins faible, de l'ordre de la centaine d'ohms pour les amplis courants. Si cette valeur paraît encore assez élevée, il faut savoir que dans un système bouclé, sa valeur sera divisée par le gain de boucle du système considéré. En pratique, l'impédance de sortie des montages sera donc couramment inférieure à l'ohm.
    Attention toutefois à la valeur de l'impédance en boucle ouverte : si on charge l'amplificateur par un condensateur (par exemple un câble coaxial assez long, ce qui peut faire plusieurs centaines de pF), la résistance de sortie couplée à ce condensateur va former un pôle supplémentaire qui peut rendre le montage oscillatoire.
  2. Vitesse de balayage (slew rate).
    En plus des problèmes de réponse en fréquence, la tension de sortie des amplificateurs ne peut pas varier instantanément d'une valeur à une autre (cas d'un échelon de tension).
    
    Fig. 31. Slew rate.
    La cause profonde vient de la structure des amplis (voir figure 28) : lors d'un transitoire violent, la capacité collecteur-base du deuxième étage doit se charger instantanément, ce qui n'est pas possible, car elle le sera par les sources de courant de polarisation. Comme ces courants sont très faibles, la charge sera relativement lente, et on note qu'elle sera linéaire (charge d'un condensateur à courant constant). On obtient le chronogramme donné figure 31.
    Cette montée linéaire en réponse à un échelon est appelée vitesse de balayage (ou plus communément slew rate) ; elle est exprimée en V/µs.
    L'ordre de grandeur du slew rate est de 0,5V/µs pour le 741, 10 à 15V/µs pour les amplis à FET du type TL081, LF356..., et peut monter à 50V/µs (voire 150V/µs avec une compensation particulière) pour le LM318.
    En général, les amplificateurs ne peuvent pas être bons partout : les amplis très précis (OP7 : fort gain en statique et très faible offset) sont souvent mauvais du point de vue slew rate, et vice versa un LM318 est bruyant et peu précis).
    Le slew rate va limiter les amplifications des forts signaux, et la bande passante sera plus faible que pour des petits signaux à fréquence donnée (la pente en V/µs des signaux est proportionnelle à leur amplitude : plus l'amplitude sera forte, plus le slew rate sera limitatif.
  3. Tension de saturation.
    On en a déjà parlé lors des montages fonctionnant en commutation : la tension de sortie est limitée à V_sat+ et V_sat-, qui sont respectivement les tensions de saturation haute et basse de l'ampli.
    Ces tension dépendent évidemment des tensions d'alimentation : elles sont inférieures aux tensions d'alimentation (en valeur absolue) d'environ 0.5 à 1.5V. Ces tensions de déchet dépendent de la température, de la charge de sortie de l'ampli (plus le courant de sortie est important, plus elles sont élevées), et de la structure de l'ampli : il existe des ampli à transistors MOSFET (LM660C de NS) spécialement conçus pour avoir une dynamique de sortie maximale, soit des tensions de déchet comprises entre 0.1 et 0.3V. On privilégiera ces amplis dans les application alimentées en monotension de faible valeur (0-5V par exemple).
    Les tensions de déchet haute et basse sont souvent différentes, ce qui fait qu'avec une alimentation rigoureusement symétrique, on aura V_sat+ |V_sat-|.
  4. Sortance en courant.
    L'impédance de sortie est une chose, la sortance en courant en est une autre : ce n'est pas parce qu'un ampli a une impédance de sortie très faible (quand il est bouclé) qu'il va pouvoir débiter des ampères !
    En pratique, les amplificateurs opérationnels sont des composants traitant des faibles signaux, pas de la puissance : les courants de sortie seront faibles, de quelques mA à quelques dizaines de mA pour les plus vaillants.
    L'amplificateur opérationnel a un étage de sortie push pull capable de fournir ou d'absorber du courant : en général, les courants maxi absorbés (sink) et fournis (source) seront sensiblement différents : on se reportera à la notice du constructeur pour plus de précisions.
    On veillera donc à ne pas trop charger les amplis en sortie (charge mini de quelques k pour des signaux de quelques volts) : on n'oubliera pas que les réseaux de contre-réaction se mettent en parallèle avec la charge de sortie ! Par conséquent, on évitera de câbler des impédances trop faibles (inférieures à une dizaine de k).
    Certains amplis sont prévus pour débiter des courants "importants" sur des charges faibles : alimenté en ±18V, le NE5534 peut débiter ±26mA dans 600 (±16V en sortie).
    Il existe aussi des amplificateurs opérationnels de puissance : la structure est la même, mais ils possèdent un étage de puissance capable de délivrer des centaines de mA voire des ampères (ex : LM12 de NS, capable de débiter ±10A). Ils sont principalement destinés aux applications audio grand public (autoradios, mini chaînes...).
  5. Protections de sortie.
    On vient de voir que les amplificateurs opérationnels ne supportent pas les forts courants ; dans ces conditions, le moindre court-circuit pourrait leur être fatal ! Heureusement, les fabricants ont inclus des protections en sortie de leurs amplis qui limitent le courant de quelques mA à quelques dizaines de mA.
    Les amplificateurs opérationnels sont ainsi des composants assez robustes, ne nécessitant pas trop de précautions d'emploi (tout est relatif...)
  6. Puissance dissipée.
    Quand un ampli débite du courant, les transistors qui le constituent (notamment ceux du push-pull de sortie) dissipent une puissance non négligeable. Les amplis encapsulés en boîtiers traditionnels (DIL8 ou CMS) peuvent dissiper entre 250mW et 1W (à 25°C). Les amplis de puissance pré-cités sont encapsulés en boîtiers de puissance (boîtiers isowatt, voire TO3 pour le LM12), et peuvent dissiper plusieurs watts, à condition bien sûr de les munir du radiateur adéquat !
    Dans tous les cas, on veillera à ne pas dépasser les limites admises par les amplis. Certains sont protégés thermiquement (limitation du courant de sortie au delà d'une certaine température), mais pas tous...
6. IMPACT SUR LES MONTAGES DE BASE.
  Tous ces "défauts" font que dans la pratique, l'amplificateur opérationnel réel s'éloigne sensiblement de l'AOP. Nous allons faire un rapide tour d'horizon de l'impact de ces défauts sur les montages de base vus plus haut, ce qui nous permettra de mieux choisir le modèle d'ampli approprié à une application donnée.
  1. Tension de saturation.
    On a vu que les tensions de saturation V_sat+ et V_sat- sont différentes : ceci aura un impact sur tous les montages en commutation où les tensions de saturation rentrent en jeu dans les formules (trigger, multivibrateur...). De plus, ces tensions vont varier avec la charge de l'amplificateur, la température... Ces défauts sont en fait assez peu gênants.
  2. Impédances d'entrée.
    L'impédance d'entrée des amplificateurs réels est dans tous les cas assez grande (>1M, rarement moins mis à part quelques amplis spéciaux). De plus, le fait que dans tous les montages linéaires l'ampli soit bouclé est bénéfique : l'impédance d'entrée est multipliée par le gain de boucle, ce qui donne facilement plusieurs dizaines ou centaines de M : on est quasiment dans les conditions de l'AOP.
    On fera tout de même attention aux montages intégrateurs, où des amplificateurs à trop faible impédance d'entrée seront rejetés, la contre réaction n'agissant pas à très basse fréquence. On préférera des amplis à entrée JFET.
  3. Offset en tension.
    C'est une des grosses tares de l'amplificateur réel. Si on doit amplifier des faibles tensions continues avec un fort gain, il faudra soit choisir un ampli à très faible offset, soit compenser un ampli standard.
    La plupart des amplificateurs possèdent deux broches destinées à régler l'offset. On se reportera à la notice du composant utilisé, les modes de branchement et les valeurs des résistances nécessaires variant d'un ampli à l'autre. Souvent, il est fait appel à un potentiomètre branché entre les deux broches d'ajustage de l'ampli et une des alimentations.
    Les amplis doubles en boîtier 8 pattes (deux amplis dans le même boîtier) ne possèdent pas de réglage d'offset. On pourra faire un montage externe, tel que celui ci-dessous :
    
    Fig. 32. Compensation d'offset d'un ampli inverseur.
    En plus de la valeur de l'offset en tension, les constructeurs donnent la valeur de sa dérive en température et dans le temps. Il est illusoire de compenser un ampli à fort offset pour faire des mesures précises, car la variation sera importante et le réglage devra être revu souvent !
    Pour faire des mesures de précision, on optera pour un "bon" ampli dès le départ !
    Pour les amplifications de tensions uniquement alternatives mais avec un fort gain (plusieurs centaines), on se méfiera aussi de l'offset : un ampli ayant 10mV d'offset (les séries TL07x et TL08x de Texas ne sont pas merveilleuse de ce point de vue !) et utilisé avec un gain de 500 délivrera une tension continue parasite de 5V en sortie ! Cette tension abaissera d'autant la plage de sortie, et on fera une correction (même sommaire) de l'offset pour résoudre ce problème.
    Le montage intégrateur sera lui aussi fortement affecté par l'offset : cette tension parasite en entrée va être intégrée et générer une rampe de tension en sortie : ce montage devra être réalisé de préférence avec un ampli à faible offset et/ou compensé.
    Les montages à seuil (comparateurs, triggers), sont bien entendus aussi affectés par l'offset, et on en tiendra compte pour des faibles signaux.
  4. Courants de polarisation.
    On a vu que les transistors de l'étage différentiel d'entrée étaient polarisés par l'extérieur ; le courant de polarisation va donc circuler dans les composants externes à l'ampli. La chute de tension ainsi provoquée va s'ajouter à l'offset en tension.
    Afin de minimiser les écarts entre les deux entrées, on veillera à ce que celles-ci "voient" les mêmes impédances.
    Pour le montage amplificateur inverseur, une compensation fréquente des effets des courants de polarisation est la suivante :
    
    Fig. 33. Compensation des courants de polarisation.
    Cet exemple montre un montage inverseur auquel on a rajouté une résistance entre l'entrée + et la masse. Cette résistance est égale à R₁//R₂, soit l'impédance vue par l'entrée -. Les deux entrées "voient" les mêmes impédances, les effets des courants de polarisation vont donc se compenser.
    Les amplis à entrée JFET sont peu concernés par ce type de compensation, du moins à faible température. En effet, on a vu que l'entrée d'un JFET était équivalente à une jonction diode en inverse. Le courant parasite doublant tous les 6°C, il peut devenir important à haute température, supérieur à ce qu'on obtient avec de bons amplis à transistors bipolaires. Pour les fortes température d'utilisation, on préférera ces derniers. Pour des usages à température ambiante, on utilisera des amplis à entrée JFET sans compensation.
    Les courants de polarisation perturbent aussi beaucoup les montages intégrateurs : pour des intégrateurs à grande constante de temps, on utilisera impérativement des amplis à entrée JFET, ou mieux MOSFET (LMC660 par exemple).
    Les montages détecteurs de seuils et échantillonneurs bloqueurs utiliseront aussi des amplis à très faibles courants de polarisation, afin de ne pas décharger le condensateur de mesure par des fuites parasites.
  5. Courants de décalage
    Les courants de décalage sont plus problématiques à compenser. Comme ils sont faibles, on se contentera d'utiliser des résistances de faible valeur pour que la chute de tension parasite soit négligeable.
  6. Plages de tensions.
    Dans tous les montages, on fera attention à ne pas dépasser les limites absolues préconisées par le fabricant de l'amplificateur utilisé. Pour les montages à commutation, où on utilise l'amplificateur avec la condition V₊V_-, on veillera à choisir des amplis tolérant une tension différentielle suffisante (entrées non bridées par des diodes).
  7. Slew rate.
    Si on doit amplifier des forts signaux à fréquence élevée, on choisira des amplificateurs à slew rate suffisant. Dans la pratique, le µA741 est trop juste (0.5Vµs) et sera délaissé au profit d'amplis à FET standards (TL081, LF356 et autres) présentant des slew rates de plus de 10V/µs.
    On choisira éventuellement des amplificateurs plus rapides pour les montages en commutation, où la sortie va devoir basculer rapidement de V_sat+ à V_sat-. On l'a déjà dit, dans ces applications, un comparateur différentiel remplacera avantageusement un amplificateur opérationnel.
    Des applications telles que les étages de sortie de convertisseurs numérique/analogique, dont la sortie varie par bonds, utiliseront aussi des amplis à fort slew rate.
RÉPONSE EN FRÉQUENCE D'UN AMPLIFICATEUR OPÉRATIONNEL. STABILITÉ.
L'amplificateur réel n'a pas un gain différentiel infini ; de plus, celui-ci varie avec la fréquence. Comme l'amplificateur est utilisé en système bouclé, sa réponse en fréquence a un impact fondamental sur la stabilité du montage, qui va aussi dépendre de la valeur de la fonction de transfert de la boucle de retour B.
Nous allons donc étudier maintenant la fonction de transfert harmonique typique d'un amplificateur opérationnel, voir quelle est la condition de stabilité d'un ampli bouclé, et étudier l'impact de ces considérations sur quelques montages de base.
Cette section ne constitue que l'aperçu d'un vaste problème qui sera approfondi en automatisme ; néanmoins, il était difficile de faire l'impasse sur une des plus grosses imperfections de l'amplificateur opérationnel et ses conséquences.
1. STABILITÉ D'UN SYSTÈME BOUCLÉ.
  Nous avons vu le principe de fonctionnement d'un système bouclé (voir figure 3) et l'expression de sa fonction de transfert :
  
  Dans le cas général, la fonction A est complexe, et comme et B sont bâtis avec des composants qui peuvent être réactifs (condensateurs notamment), ces deux fonctions vont aussi être complexes : on va pouvoir déterminer le module du gain et le déphasage entrée/sortie en fonction de la fréquence (c'est la représentation de bode : nous n'utiliserons que celle-ci, contrairement à l'automatisme dont les adeptes sont friands d'autres critères beaucoup plus complexes à appréhender et moins intuitifs à comprendre !).
  1. Ordre d'un système
    L'ordre d'un système est déterminé par le nombre de pôles de sa fonction de transfert (les valeurs de la fréquence qui annulent le dénominateur).
    Ces pôles peuvent être réels ou imaginaires, et ainsi, l'ordre du système est donné par le degré du polynôme en f (ou , ce qui revient au même) qui forme le dénominateur de la fonction de transfert.
    Le tracé asymptotique du gain dans le plan de bode va être fonction de l'ordre du système (voir figure 34) : un système d'ordre 1 aura une pente de -20dB/décade au delà de la fréquence de cassure déterminée par son pôle, un système d'ordre 2 une pente de -40dB/décade... Chaque pôle supplémentaire augmente la pente de -20dB/décade.
    Parallèlement au gain, la phase diminue de -90° à chaque pôle. Les -180° fatidiques sont atteints asymptotiquement pour l'ordre 2.
    La figure 34 illustre un système à deux pôles (10Hz et 10kHz), dont la fonction de transfert est la suivante :
    
    Sur ce graphique, on a fait un tracé asymptotique du gain, qui met bien en évidence les pôles (fréquences de cassures) et les pentes de décroissance du gain.°
    Jusqu'à 1kHz environ, la phase varie comme pour un système du premier ordre (asymptote à -90°), et ensuite, à cause du deuxième pôle, elle tombe à -180° (valeur asymptotique qui ne sera théoriquement jamais atteinte).
    
    Fig. 34. Système à deux pôles.
    Un système du premier ordre sera toujours stable (phase mini de -90°), et les ennuis vont commencer dès le deuxième ordre (dépassements, oscillations amorties...). Il faut un troisième pôle pour arriver aux conditions d'oscillations, mais dans les amplificateurs opérationnels, on trouve toujours ce pôle supplémentaire, soit en interne, soit dans les composants externes (câblés volontairement ou parasites).
    Ce troisième pôle, même placé assez loin du deuxième, abaissera suffisamment la phase pour que les conditions d'oscillation soient réunies.
  2. Condition de Barkhausen.
    Si on regarde l'expression [70], on voit que le produit AB peut être négatif, et notamment prendre la valeur -1 (le module du gain vaut 1 et le déphasage est de -180°).
    Dans ce cas particulier, le dénominateur s'annule : il n'y a plus besoin de signal en entrée pour qu'il existe un signal en sortie. Nous avons réalisé un oscillateur ; un exemple sera décrit plus loin.
  3. Réponse en transitoires.
    Si dans certains cas, le fonctionnement en oscillateur du système bouclé est voulu, il sera indésirable la plupart du temps.
    Un système ne passera pas ex-abrupto de l'état stable aux conditions d'oscillation de Barkhausen. Le phénomène sera progressif, et, sur des transitoires marqués (ex : échelon de tension), le signal de sortie présentera un dépassement (overshoot) de plus en plus important, accompagné d'oscillations de moins en moins amorties au fur et à mesure que l'on va se rapprocher de la condition de Barkhausen.
    Ces dépassements et oscillations vont beaucoup perturber le fonctionnement de l'amplificateur, et modifier de façon substantielle le signal à amplifier : même si le système n'est pas un oscillateur, il n'en est pas moins inutilisable.
    La figure 35 illustre ce propos : elle représente la réponse indicielle (réponse à un échelon unité de tension) de trois systèmes bouclés dont les marges de phase sont respectivement de 18, 39 et 51° (par rapport aux 180° de l'oscillateur). Plus la marge de phase diminue, plus les oscillations et les dépassements sont forts (60% de dépassement pour une marge de 18°).
    
    Fig. 35. Réponse indicielle de systèmes bouclés.
    On y voit aussi que même pour une marge correcte du point de vue critère de stabilité (soit >45°), on a un léger dépassement (mais très peu d'oscillations).
    Le processus d'instabilité est donc progressif, et augmente au fur et à mesure qu'on se rapproche de la limite d'oscillation.
  4. Critères de stabilité.
    En pratique, on a vu que l'étude de la stabilité va se résumer (dans notre cas : ne généralisons pas à tous les systèmes !) à l'analyse du produit AB (le gain de boucle). Deux méthodes simples vont consister à regarder la phase ou la pente de la courbe de gain pour un module du gain égal à 1.
    - Marge de phase.
      Le critère généralement retenu par les automaticiens pour que le système soit déclaré stable est que la phase ne doit pas être inférieure à -135° pour un module |AB|=1 . Il reste une marge de 45° pour atteindre les 180° fatidiques (oscillateur). On dit que la marge de phase est de 45° .
    - Pente de la courbe de gain.
      Un critère très simple de stabilité sera le suivant : le diagramme asymptotique du produit AB devra croiser l'axe 0dB avec une pente maximum de -20dB/décade . Toute pente supérieure dénotera un système instable.
    - Choix du critère de stabilité.
      Il convient de noter ici que le critère de la pente est très facile à mettre en œuvre, car le seul tracé asymptotique est nécessaire, et que ce tracé nécessite peu de calculs (uniquement les fréquences de cassure des divers pôles et zéros de la fonction de transfert).
      Dans le cas de compensation de plusieurs pôles par plusieurs réseaux de compensation, il se peut que ce critère soit insuffisamment précis : on l'utilisera pour "dégrossir" le problème et mettre en place les réseaux de compensation adéquats, et on optimisera ces réseaux en appliquant le critère de marge de phase, plus précis.
      Pour un système compliqué, le tracé précis de la phase nécessite un calcul complet, qui peut vite se révéler laborieux à la main : un logiciel de tracé de courbes travaillant en complexes est quasiment nécessaire.
2. FONCTION DE TRANSFERT DES AMPLIFICATEURS OPÉRATIONNELS.
  Il existe deux principaux types d'amplificateurs sur le marché :
  les amplificateurs inconditionnellement stables : le montage amplificateur est stable quel que soit le gain en boucle fermée obtenu (jusqu'au gain unité). Pour un gain supérieur à 0dB, ces amplificateurs présentent une réponse en fréquence du type premier ordre (pente de -20dB/décade), d'où leur stabilité inconditionnelle.
  certains amplificateurs à hautes performances présentent un deuxième pôle dans leur fonction de transfert pour des gains supérieurs à l'unité. De ce fait, en amplification pure (le réseau de retour est constitué de résistances, d'où B est réel), le système bouclé sera stable uniquement pour un gain supérieur à une certaine valeur (typiquement 5). Leur domaine d'utilisation est donc différent : ils possèdent de meilleures performances en fréquence que les premiers au prix d'une interdiction de leur emploi (sans précautions particulières) dans certaine fonctions.
  Pratiquement, les fonctions de transfert des amplificateurs sont similaires à celles représentées en annexe 3 pour les amplis inconditionnellement stables et annexe 4 pour les amplis dits "décompensés".
  On remarque que le gain en statique (pour une fréquence nulle, soit le continu) est très élevé, mais, le premier pôle réduit ce gain à partir d'une fréquence très basse (de quelques hertz à quelques dizaines d'hertz).
  Le deuxième pôle est situé beaucoup plus loin : vers 1Mhz pour le µA741, 4Mhz pour les TL081, LF356...
  En fait, dans les amplis inconditionnellement stables, on place volontairement le premier pôle très bas en fréquence (c'est le rôle du condensateur C du schéma de la figure 28), de manière à ce que le gain ait chuté suffisamment pour couper l'axe 0dB avant la deuxième fréquence de cassure.
  De cette manière, pour des gains en boucle fermée jusqu'à 0dB, le système est du premier ordre, et ne sera donc jamais oscillatoire.
  On agit sur le premier pôle, car il est plus difficile technologiquement de reculer le deuxième (et le troisième qui n'est pas loin !) : c'est le cas des amplificateurs rapides, et ils sont chers et délicats à utiliser...
  Pour améliorer le gain aux fréquences élevées, on diminue la valeur de la capacité intégrée C : on déplace le premier pôle d'un facteur 5 sur l'axe fréquentiel, et on atteint alors le deuxième pôle pour un gain de l'ordre de 5 avec les amplis courants (LF357, qui est un LF356 décompensé, LM149, qui est un LM148 décompensé, OPA637, qui est un OPA627 décompensé...).
  L'amplificateur n'est plus inconditionnellement stable, et ne pourra pas servir dans des applications telles que les suiveurs, dérivateurs, filtres d'ordre 2, montages logarithmiques, redresseurs sans seuils... En revanche, il fera merveille pour des amplis à fort gain : la bande passante sera 5 fois plus élevée qu'avec l'ampli équivalent inconditionnellement stable.
3. AMPLIFICATEUR BOUCLÉ. PRODUIT GAIN-BANDE.
  Lorsqu'on boucle un ampli non inverseur avec un réseau de résistances, tant que le gain de boucle AB est élevé (soit à basse fréquence), le gain du système bouclé va tendre vers 1/B (voir [4] ; est égal à 1 dans ce cas) ; à haute fréquence, le gain de boucle va diminuer, pour devenir égal, puis inférieur à la valeur 1/B. Dans ces conditions, la courbe de réponse en fréquence du système bouclé va tendre asymptotiquement vers celle de l'amplificateur.
  
  Fig. 36 Amplificateur bouclé.
  La figure 36 donne le résultat obtenu avec un ampli du type µA741 (première cassure à 10Hz, deuxième à 1MHz, gain statique de 100dB).
  Si on observe cette figure, on remarque que le produit du gain par la bande passante à -3dB est constant, et égal ici à 1MHz, soit la fréquence pour laquelle le gain en boucle ouverte vaut 1 (0dB).
  Ce produit est une caractéristique importante de l'amplificateur pour caractériser ses performances en fréquence.
  Ex : 1MHz pour le µA741, 3MHz pour le TL081, 15MHz pour le LM318...
  On note que cette caractéristique est juste pour les amplis inconditionnellement stables. Pour les amplis décompensés, la fréquence théorique à gain unité est obtenue en prolongeant la droite à -20dB/décade située entre la première et la deuxième cassure jusqu'à l'axe 0dB.
4. COMPENSATION EN FRÉQUENCE.
  Tout le travail de compensation en fréquence de l'amplificateur consistera à installer des réseaux de correction de telle manière que la condition de coupure à -20dB/décade soit réalisée. Cette méthode sera préférée aux autres, car elle est très simple à mettre en œuvre, et l'effet des réseaux correcteurs sur le tracé de bode est bien visible.
  1. Compensation par déplacement de la première fréquence de cassure.
    Cette méthode est extrêmement simple ; elle est un prolongement de l'astuce technique qui consiste à placer le condensateur C (voir le schéma de la figure 28) entre collecteur et base du transistor du deuxième étage de l'ampli. La figure 37 montre le diagramme de bode asymptotique permettant de comprendre la compensation qui consiste à rajouter une capacité supplémentaire en parallèle avec la capacité C de la figure 28. (deux broches sont disponibles sur les boîtiers des amplis prévoyant cette compensation). De ce fait, la première fréquence de cassure recule vers les basses fréquences.
    Ces compensations étaient nécessaires avec des amplis anciens (LM101 par exemple) qui étaient bâtis pour garantir de bonnes performances à haute fréquence, mais nécessitaient une compensation pour les applications à faible gain.
    
    Fig. 37. Compensation d'un ampli à gain unité.
    L'astuce est très simple, et consiste à reculer toute la partie haute du diagramme de bode pour que le produit AB coupe l'axe 0dB dans la zone à -20dB/décade (ici, on coupe juste à la limite du deuxième pôle, la marge de phase est de 45°).
    Sur le schéma, on a représenté la compensation d'un montage suiveur : B vaut 1, et le produit AB se confond avec A, gain en boucle ouverte de l'ampli : n'oublions pas que le critère de stabilité s'applique au produit AB !
    On note l'overshoot de 10dB pour le montage suiveur non compensé, garant de fortes oscillations sur les transitoires. Le suiveur compensé a une courbe quasi-plate, mais en revanche, a une bande passante plus faible.
    Ce montage présente deux gros inconvénients :
    le gain de boucle est réduit dès les plus basses fréquences, ce qui nuit à la précision.
    le slew rate est affecté : la capacité de compensation vient se mettre en parallèle sur C ; l'ensemble, de capacité supérieure à C, va se charger avec le même courant, donc plus lentement.
    Avec l'apparition d'amplis rapides inconditionnellement stables, ce type de compensation est devenu peu utilisé.
  2. Compensation par retard de phase.
    On a imaginé une autre méthode de compensation éliminant les défauts de la méthode précédente : on ne va pas reculer la première fréquence de cassure, mais on va déformer la courbe de réponse en fréquence plus loin, par adjonction d'un réseau à retard de phase dans la chaîne directe de l'asservissement (en cascade avec A).
    Le but est de faire chuter le gain rapidement (avec une pente de -40dB/décade), pour reprendre ensuite une pente de -20dB/décade un peu avant que le produit AB ne croise l'axe 0dB : même si la pente a été de -40dB/décade auparavant, le montage est stable quand même, car le point important est que l'axe 0dB soit croisé avec une pente de -20dB/décade.
    Attention : si on veut augmenter le gain en boucle fermée du montage (par exemple, montage à gain réglable), il faut garder à l'esprit qu'on va abaisser la valeur globale du produit AB, et qu'on va se retrouver à un moment donné avec un croisement de l'axe 0dB avec une pente de -40dB/décade : le montage ne sera pas stable dans toute une plage de gain !
    C'est le prix à payer d'une amélioration du gain aux basses fréquences, la compensation par recul de la première fréquence de cassure n'avait pas ce défaut...
    
    Fig. 38 Compensation par retard de phase.
    Comment réaliser le réseau à retard de phase susceptible de modifier le gain de la chaîne directe ? Il faut tirer parti des éléments existants du montage, y compris des éléments parasites. Dans les amplificateurs de puissance (HIFI et autres, dont on a dit que la structure est la même que celle des amplificateurs opérationnels), on utilise l'impédance de sortie en boucle ouverte pour créer le réseau suivant :
    
    Fig. 39 Réseau à retard de phase.
    Sa réponse en fréquence est la suivante (représentation du gain réel et du gain asymptotique du réseau utilisé dans la compensation illustrée figure 38) :
    
    Fig. 40. Réponse en fréquence du réseau à retard de phase.
    La fonction de transfert de ce réseau est de la forme :
    
    avec :
    
    Dans le réseau de la figure 39, la résistance R₁ est en fait souvent l'impédance de sortie d'un étage amplificateur qu'on cherche à compenser. On trouve ainsi très souvent un réseau R-C série en sortie des amplificateurs HIFI : ce réseau est destiné à les stabiliser avec une compensation par retard de phase. Ce procédé n'est pas utilisé tel quel sur les amplificateurs opérationnels : le réseau R-C chargerait trop la sortie de l'amplificateur.
  3. Compensation par avance de phase.
    La compensation par retard de phase n'est pas très simple à mettre en œuvre dans les montages à amplificateurs opérationnels. On lui préférera souvent la compensation par avance de phase, qui possède les avantages suivants :
    simple à mettre en œuvre (un condensateur supplémentaire suffit souvent).
    bande passante élargie par rapport aux autres modes de compensation.
    slew rate non altéré.
    Le défaut est que cette compensation n'est possible simplement qu'avec des gains supérieurs à 2 ou 3 (montage suiveur incompensable par cette méthode).
    Jusqu'à maintenant, on n'a pas touché la deuxième fréquence de cassure du produit AB (qui est celle de A en amplification pure). C'est ce qu'on va faire ici.
    Il existe deux méthodes :
    reculer la deuxième fréquence de cassure de l'ampli (compensation feed-forward) : cette méthode est assez délicate à mettre en œuvre, et ne fonctionne pas pour tous les montages.
    augmenter la valeur de B à haute fréquence : il suffit de jouer sur le réseau de contre réaction, ce qui est beaucoup plus simple (mais nécessite un gain du système bouclé supérieur à 2 ou 3).
    La figure 41 montre la compensation par un tel réseau d'un ampli ayant un gain en boucle fermée de 10dB. On remarque qu'aux basses fréquences, B vaut -10dB (B est un atténuateur !), et qu'à partir d'une fréquence un peu supérieure à la deuxième fréquence de cassure de l'ampli, sa valeur remonte, pour tangenter ensuite l'axe 0dB (la figure montre le diagramme asymptotique de B).
    Grâce à ce réseau, la courbe du produit AB peut s'étendre vers les fréquences élevées, jusqu'à tangenter la courbe A de l'ampli en boucle ouverte, qui constitue une limite ; cette remarque explique pourquoi on ne peut pas compenser avec cette méthode un ampli de gain unité, le produit AB étant confondu dans ce cas avec A.
    
    Fig. 41. Compensation par avance de phase.
    Le réseau à avance de phase peut être construit de la manière suivante :
    
    Fig. 42. Réseau à avance de phase.
    La fonction de transfert de ce réseau est du type :
    
    avec :
    
    Le fonctionnement de ce réseau est simple : aux hautes fréquences, C vient shunter R₁, et V_s tend vers la valeur de V_e : le pont diviseur passe de la valeur R₂/(R₁+R₂) à 1.
    Sur un montage du type amplificateur non inverseur, ce réseau est extrêmement simple à mettre en œuvre : on se contentera de rajouter un condensateur C en parallèle avec la résistance R₁ :
    
    Fig. 43. Ampli non inverseur compensé.
    L'avantage de ce montage, c'est qu'on peut le compenser très simplement sans aucun calcul, en expérimentant des valeurs de C directement sur le montage attaqué par un signal carré en entrée : la bonne valeur du condensateur est celle qui réduit l'overshoot et les oscillations parasites à une valeur convenable.
    C'est ce que faisaient beaucoup de "bidouilleurs" à la belle époque de l'électronique analogique, sans connaître en détails la justification théorique de leur expérimentation.
  4. Bilan des compensations.
    On a vu trois méthodes de compensation :
    la compensation par déplacement du premier pôle est simple à mettre en œuvre, universelle, et donne un amplificateur inconditionnellement stable une fois compensé. Les défauts sont une bande passante rétrécie, donc un gain de boucle diminué dès les plus basses fréquences, et un slew rate ralenti.
    la compensation par retard de phase dans la chaîne directe est moins simple à appliquer sur des montages à amplificateurs opérationnels, mais très utilisée sur des amplificateurs de puissance. L'amplificateur résultant n'est pas inconditionnellement stable, et cette compensation nécessite des calculs et tracés de bode pour être efficace. Elle doit être adaptée au cas par cas. Il existe divers montages de compensation ; certains n'ont pas d'effet sur le slew rate (cas décrit ci-dessus), d'autres le diminuent.
    la compensation par avance de phase dans la boucle de retour est simple à utiliser, et son côté intuitif lui permet de trouver la bonne compensation rapidement par expérimentation. Le slew rate n'est pas affecté, la bande passante est meilleure qu'avec les autres méthodes, mais, elle est inapplicable pour un gain unité.
5. ÉTUDE DE STABILITÉ DE MONTAGES SIMPLES.
  1. Amplificateur rapide.
    Il peut paraître stupide d'utiliser un amplificateur rapide à faible coût (ampli décompensé type LF357) pour l'utiliser avec des faibles gains. En fait, il ne faut pas oublier que le slew rate de ce type d'ampli est beaucoup plus élevé que celui du même ampli inconditionnellement stable (12V/µs pour le LF356, 50V/µs pour le LF357...).
    Il peut donc valoir la peine d'utiliser un ampli rapide et de le compenser, par exemple par réseau à avance de phase dans la boucle de retour. L'annexe 5 montre un tel montage et sa réponse en fréquence et en phase, qui illustre bien la compensation.
  2. Montage dérivateur.
    Même avec un ampli inconditionnellement stable, le montage dérivateur est oscillatoire. En rajoutant simplement une résistance en série avec le condensateur, on stabilise le tout, sachant qu'on limite évidemment la plage où le montage est dérivateur : on ne peut pas tout avoir ! Le schéma et le mécanisme de compensation sont exposés en annexe 6.
6. OSCILLATEURS.
  1. Oscillateur à pont de wien.
    On a vu que quand le dénominateur de la fonction de transfert s'annule, le système devient auto-oscillant.
    La condition de Barkhausen s'écrit :
    
    Le produit AB doit donc être égal à -1 : cela correspond à une phase de ±180° pour un module du gain égal à 1.
    B étant en général un réseau passif (c'est la solution la plus simple, mais il existe aussi des réseaux de retour actifs), il sera atténuateur. La valeur du module de l'amplification A devra donc être supérieure à 1 pour compenser cet te atténuation et faire en sorte que |AB|=1.
    La phase de 180° peut provenir soit de l'ampli (ampli inverseur : la phase de B doit dans ce cas être égale à 0), soit du réseau B (ampli non inverseur dans ce cas)
    Il existe plusieurs réseaux produisant un déphasage de 0° ou 180° ; un des plus utilisés est le réseau de Wien :
    
    Fig. 44. Pont de Wien.
    La réponse en fréquence de ce réseau est la suivante :
    
    Fig. 45. Réponse en fréquence du pont de Wien.
    La phase de ce réseau varie de +90° à -90° , et passe par la valeur 0° lorsque le gain atteint une valeur maxi de -9,54dB, qui correspond à une atténuation de 3.
    La fonction de transfert de ce réseau s'écrit :
    
    Le maximum de B est atteint pour :
    
    Pour satisfaire aux conditions de Barkhausen, il faut donc mettre ce réseau en contre-réaction d'un amplificateur de gain -3 ; une autre solution possible est de reboucler avec ce réseau non pas sur l'entrée - de l'ampli, mais sur l'entrée + : avec un gain de +3, les déphasages sont les mêmes. Le schéma obtenu est le suivant :
    
    Fig. 46. Oscillateur à pont de Wien.
    La structure est simple à comprendre : il s'agit d'un amplificateur non inverseur, avec le pont de Wien rebouclé sur l'entrée de ce type d'ampli, donc, l'entrée +.
    En pratique, on remplacera R₁ ou R₂ par une résistance ajustable, et on augmentera le gain progressivement jusqu'à l'apparition d'oscillations en sortie du montage. Au fur et à mesure que le gain se rapproche de +3, la fonction de transfert globale du montage va tendre vers l'infini, comme illustré sur la figure 47 :
    
    Fig. 47. Fonction de transfert de l'oscillateur.
    Cet oscillateur, quand il est bien réglé, donne un signal sinusoïdal avec très peu de distorsion.
    En pratique, pour limiter l'amplitude des oscillations, on devra introduire un élément non linéaire dans la chaîne : soit des diodes zéner en sortie, soit une lampe à filament spécialement prévue pour cet usage à la place de R₁.
    Si le gain devient supérieur à 3, les oscillations prennent une amplitude telle qu'elles sont écrêtées par l'amplificateur. Le signal n'est plus franchement exploitable, car il présente une distorsion importante.
    Les oscillateurs sont délicats à mettre en œuvre, car il faut les régler de telle manière que le gain soit suffisant pour que l'oscillateur "accroche", mais pas trop grand, car on a alors beaucoup de distorsion. La plage de fonctionnement correcte est très étroite, et relativement instable (variations dues à la température, à la charge de l'ampli...).

[ Table des mati�res ]