Convertisseurs A/N et N/A

INTRODUCTION.

L'électronique est divisée en deux domaines distincts :
- le domaine analogique , où les variables peuvent prendre une infinité de valeurs différentes ; les signaux varient continûment. Tous les signaux issus des capteurs sont analogiques, et traduisent des phénomènes physiques qui varient continûment.
- le domaine numérique , où les variables prennent uniquement deux états, un état haut et un état bas.
Le domaine numérique est maintenant prédominant. Il s'est beaucoup développé grâce aux progrès faits par les microprocesseurs. Beaucoup de signaux naguère traités de façon analogiques le sont aujourd'hui par programmation de microprocesseurs.
Le gros avantage apporté par la numérisation des signaux est la possibilité de stockage, de transformation et de restitution des données sans qu'elles ne soient altérées. On peut par exemple faire transiter un signal sonore de qualité HI-FI par une ligne téléphonique sans que la bande passante réduite ni le bruit de cette ligne ne soient gênants, ce qui aurait été impensable avec le signal analogique de départ !
Le traitement des données par programmation introduit aussi une souplesse dans la conception de produits à base d'électronique : un même circuit électronique à base de P pourra traiter des signaux différents ; seul le programme va changer. Cela permet de réduire les coûts par standardisation, la même carte étant utilisée pour plusieurs fonctions différentes. L'électronique analogique nécessitait au mieux un changement des composants, au pire, la conception d'une nouvelle carte.
Mais, à la base, les signaux ont toujours une nature analogique ! Il faut donc les amplifier et éventuellement les extraire de signaux parasites (tension de mode commun par exemple). Le domaine analogique va donc toujours exister au moins en amont de toute chaîne de traitement. Parfois, on a aussi besoin d'un signal analogique en sortie de cette chaîne de traitement : il faudra alors reconvertir les données numériques en signal analogique.
Le passage d'un type de donnée à l'autre se fera par des convertisseurs, composants " mixtes " qui vont manipuler des tensions analogiques en entrée et des signaux logiques en sortie ou vice versa.
Il existe deux catégories de convertisseurs :
- les Convertisseurs Analogique Numérique (CAN, ADC en anglais, pour analog to digital converter), qui vont transformer les tensions analogiques en signaux logiques aptes à être traités par microprocesseur (numérisation des signaux).
- les Convertisseurs Numérique Analogique (CNA, DAC en anglais, pour digital to analog converter) qui vont convertir les signaux logiques en tension analogique.
Plusieurs types de convertisseurs sont disponibles dans chaque catégorie, qui se différencient par leur précision, leur vitesse de traitement de l'information, leur prix...
Il n'y a pas " le " convertisseur à tout faire qui soit bon partout : on devra faire un choix en fonction de ses besoins.
- Exemple de chaîne de traitement.
  
  Un exemple très répandu de conversion et traitement de données est la chaîne de transformation du son, de l'enregistrement de la musique à sa restitution par les enceintes acoustiques.
  Le son est capté par des micros, dont la très faible tension de sortie est amplifiée. Le signal peut être numérisé directement à ce niveau, et sera alors traité de façon entièrement numérique (mixage...). Il peut aussi être stocké de façon analogique sur bande magnétique, mixé, et ensuite numérisé. L'avantage du traitement numérique réside dans le fait que les données sont inaltérables, contrairement aux données analogiques stockées sur bande magnétique : celle-ci se dégrade lors des passages répétés sur les têtes de lecture.
  Le stockage est maintenant presque toujours numérique (compact disc). Le lecteur de CD contient des convertisseurs numérique analogique qui vont retransformer les informations numériques en signal analogique qui sera amplifié avant d'être envoyé aux enceintes.
NOTIONS GÉNÉRALES.
1. CONVERSION ANALOGIQUE/NUMÉRIQUE.
  1. Principe de fonctionnement.
    
    On a vu dans l'introduction que les signaux numériques ne varient pas de façon continue. En fait, quand on voudra numériser un signal analogique (donc continu), il va falloir le discrétiser sur deux dimensions : le temps et l'amplitude.
    Il est impensable de décrire un signal avec une infinité de valeurs ; on va le mesurer à des instants bien déterminés : c'est ce qu'on appelle l'échantillonnage .
    Pour ce qui est de l'amplitude, à un intervalle de tension du signal d'entrée on fera correspondre une valeur unique : c'est la quantification (voir figure 1). Cette valeur sera ensuite codée (binaire, binaire signé...) et restituée sous forme binaire en sortie du convertisseur pour être traitée par de l'électronique numérique.
    
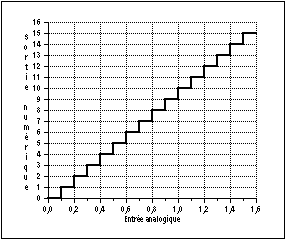
    Fig. 1. Fonction de transfert d'un CAN.
    La figure 1 représente la fonction de transfert d'un CAN, à savoir le code numérique de sortie en fonction de la tension d'entrée. On y voit clairement les plages de tension associées à un état numérique de sortie :
    V_log = 0 pour 0 V_e < 0,1V
    V _log = 1 pour 0,1 V_e < 0,2V
    V _log = 6 pour 0,6 V_e < 0,7V ...
    L'étape de quantification de la conversion analogique numérique entraîne une perte d'information.
    Un résumé graphique de tout ceci est exprimé sur la figure 2 : on y voit un signal analogique en entrée (une sinusoïde), et les échantillons issus de la conversion analogique numérique, avec la double discrétisation mentionnée.
    
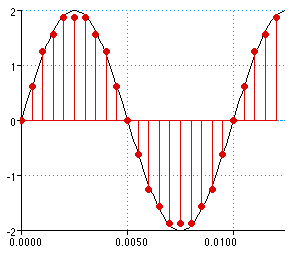
    Fig. 2. Signal analogique et numérisé
  2. Définitions.
    
    Nous allons donner ci-dessous plusieurs définitions théoriques ; afin de bien comprendre à quoi elles correspondent dans la réalité, un exemple de convertisseur 3 bits est exposé plus loin. Le lecteur est invité à consulter les deux paragraphes en parallèle.
    Toutes ces définitions sont données pour des convertisseurs parfaits ; en pratique, on est loin du compte, car ces composants intègrent des comparateurs différentiels, amplificateurs opérationnels et autres réseaux de résistances qui sont imparfaits. Nous allons lister ensuite les principaux défauts des convertisseurs.
    - Plage de conversion.
      
      Le convertisseur délivrera en sortie un nombre fini de codes numériques, correspondant à une gamme de tension analogique d'entrée bornée : c'est la plage de conversion (ou tension de pleine échelle) du convertisseur. Cette plage de conversion sera couramment de 0-5V, 0-10V, ou encore ±5V ou ±10V. Il existe aussi d'autres plages de conversion moins usitées.
    - Résolution.
      
      Le signal numérisé sera d'autant plus riche en information que l'intervalle de tension qui sera codé par le même nombre binaire sera petit, et ceci à plage de conversion donnée.
      La résolution du CAN sera l'intervalle de tension d'entrée à laquelle correspondra un même nombre binaire.
      En théorie, cet intervalle de tension est le même pour tous les codes binaires ; en pratique, ça ne sera pas toujours le cas (voir les erreurs de conversion). La résolution correspondra à la valeur théorique.
    - Dynamique.
      
      La dynamique d'un signal est le rapport entre la tension maxi et la tension mini que pourra prendre ce signal.
      Pour un CAN, ce sera le nombre binaire le plus élevé divisé par le plus faible qui est 1 (et pas 0 qui correspond à un signal nul), donc, le nombre de codes binaires différents que peut fournir le convertisseur moins un (le zéro !).
      Si on prend l'exemple d'un convertisseur 8 bits, la dynamique vaut en toute rigueur 2⁸ - 1 = 255.
      En pratique, on arrondira ce nombre à une puissance de 2, qui sera le nombre de bits du convertisseur. Notre convertisseur aura donc une dynamique de 256, qu'on exprimera plutôt sous la forme " 8 bits ", ou encore 48db = 20log(256).
    - Mise en relation.
      
      Il est possible de relier la dynamique, la résolution et la plage de conversion d'un convertisseur.
      La résolution correspond à la variation d'une unité du code binaire ; cette unité est égale à la variation du bit de poids le plus faible (LSB = least significant bit en Anglais). Si on désigne par V_MAX la plage de conversion et N le nombre de bits du convertisseur, on a la relation :
      
      L'exemple suivant clarifiera cette relation.
  3. Exemple : CAN 3 bits
    
    Fig. 3. Fonction de transfert d'un CAN 3 bits
    Sur la figure 3, on a représenté la fonction de transfert d'un CAN à 3 bits ayant une plage de conversion de 8V. Il y a 8 états logiques, la plage de conversion est donc partagée en 8 portions égales correspondant chacune à un état logique de sortie.
    On remarquera que la dernière transition du CAN se fait pour une tension d'entrée de 7V, correspondant au dernier état logique de sortie (égal à 7).
    Passée cette valeur de 7V, le convertisseur ne changera donc plus d'état. Toutefois, on considère que la plage de conversion s'étend jusqu'à 8V, la dernière portion, de 7 à 8V correspondant à l'état logique " 7 ".
    Dans ces conditions, la plage de conversion est de 8V, divisée en 2³ = 8 portions correspondant chacune à un LSB valant 8V/8=1V. On retrouve le résultat de l'équation [1].
  4. Erreur de quantification. Amélioration.
    
    On a déjà dit que la double quantification, dans le temps et en amplitude consistait en une perte d'information du signal. Ceci nous conduit à la notion d'erreur de quantification, qui est inhérente à la conversion analogique/numérique (et inverse), et sera présente même si les convertisseurs sont considérés comme parfaits. Cette erreur systématique s'ajoute donc aux erreurs décrites plus loin.
    Si on numérise une rampe de tension, l'erreur entre la tension d'entrée et la tension de sortie " reconstituée " (reconvertie en analogique par passage dans un CNA) aura la forme suivante :
    
    Fig. 4. Erreur de quantification d'un CAN.
    L'erreur est toujours négative (valeur par défaut), et oscille entre 0 et -1 LSB (0 à -1V ici).
    Il serait souhaitable d'avoir plutôt une erreur centrée autour de 0, de manière à quantifier tantôt par excès, tantôt par défaut ; en effet, en quantifiant systématiquement par défaut, on introduit un offset dans le signal numérisé.
    Pour pallier cet inconvénient, on introduit un décalage au niveau du premier LSB du convertisseur, comme indiqué sur la figure 5 : la première transition n'a pas lieu pour 1 LSB, mais pour 1/2 LSB seulement, ce qui fait que jusqu'à une valeur d'entrée inférieure à 1/2 LSB, on quantifie par défaut, et entre 1/2 et 1 LSB, on quantifie par excès.
    
    Fig. 5. Fonction de transfert d'un CAN 3 bits corrigé.
    L'erreur obtenue devient celle de la figure 6 : elle est symétrique par rapport à 0 et égale à ±1/2 LSB.
    
    Fig. 6. Erreur de quantification symétrique
    Il y a juste une exception : le 1/2 LSB tronqué au début va se retrouver en bout d'échelle (voir figure 5) : le dernier état numérique correspondra à une plage d'entrée analogique valant 1 1/2 LSB. L'erreur de quantification sera plus grande sur cette plage, ce qui n'est d'ailleurs pas très grave !
    En pratique, la majorité des CAN ont une fonction de transfert décalée pour assurer une erreur de quantification symétrique. Il faudra toutefois s'en assurer en lisant la spécification du constructeur.
    Ce détail pourra être important si on fait de la mesure précise avec une carte d'acquisition de donnée (comprenant un CAN). Pour régler le gain et l'offset de la chaîne de conversion, il faudra observer la première et la dernière transition, et la calibration sera différente si le convertisseur est décalé ou pas ; un biais d'1/2 LSB pourra fausser les mesures si on se trompe !
2. CONVERSION NUMÉRIQUE/ANALOGIQUE.
  1. Principe de fonctionnement.
    
    Si on fait l'opération inverse (conversion numérique analogique), à chaque valeur numérique, on fera correspondre une valeur analogique (et une seule) ; la tension analogique de sortie variera par " bonds ", et non plus continûment comme dans le signal d'origine. La fonction de transfert sera la même que celle de la figure 1 mais inversée. La tension de sortie aura une forme d'escalier. En pratique, on va filtrer cette tension pour lisser ces discontinuités et essayer de se rapprocher au mieux du signal d'origine (Figure 7).
    
    Fig. 7. Conversion numérique analogique.
  2. Définitions.
    - Résolution.
      
      La résolution du CNA sera la variation de tension de sortie correspondant à la variation d'une unité du nombre binaire en entrée. La définition est équivalente à celle du CAN.
    - Plage de conversion.
      
      Il y a ici une petite différence avec le CAN (voir figure 8) : la plage de conversion numérique va de 0 à 2^N-1, N étant le nombre de bits du convertisseur, et à chaque valeur numérique correspond une valeur analogique de sortie et une seule. Par rapport à celle du CAN, la plage de conversion s'arrêtera donc un LSB plus tôt (sur l'échelle analogique du CAN, ceci correspond à la dernière transition numérique).
      Nous sommes ramenés ici au vieux problème des poteaux et des intervalles !
    - Dynamique.
      
      La définition est équivalente à celle du CAN.
    - Mise en relation.
      
      Vu ce qui a été dit sur la plage de conversion, la relation entre le pas de quantification (1 LSB), la plage de conversion V_MAX , et le nombre de bits du convertisseur sera légèrement différente de l'équation [1]. La figure 8 du paragraphe suivant va éclairer cette équation :
      
      En pratique, pour un nombre de bits supérieur à 8, l'écart entre les deux formules reste très faible !
      Il n'empêche que dans le cas de mesures précises, ce genre de détail a son importance pour expliquer un biais inattendu.
  3. Exemple : CNA 3 bits.
    
    Fig. 8. Fonction de transfert d'un CNA 3 bits.
    La figure 8 montre la fonction de transfert d'un CNA 3 bits ayant une résolution de 1V, comme l'exemple de CAN donné précédemment.
    On voit clairement ici ce qui a été dit pour la plage de conversion : la plage s'étend de 0 à 7V, et non pas 8V comme pour le CAN, car le dernier état numérique est " 7 ".
3. ERREURS DE CONVERSION.
  
  Les erreurs décrites dans les paragraphes 1 à 3 sont valables pour les CAN comme pour les CNA. Les illustrations sont faites pour ces derniers, mais sont facilement transposables.
  1. Erreur de gain.
    
    La tension de pleine échelle est toujours légèrement différente de ce qui est prévu en théorie. L'écart entre les valeurs théorique et pratique est l'erreur de gain (figure 9).
    Pratiquement, le fabricant de convertisseurs Analog Devices définit cette erreur ainsi : c'est l'écart entre la valeur théorique et la valeur réelle mesurée sur la dernière transition du convertisseur et exprimé en LSB. Cette mesure suppose que l'ajustage du zéro soit parfait.
    
    Fig. 9. Erreur de gain.
  2. Erreur d'offset.
    
    De même, le code binaire 0 ne correspond pas forcément à une tension rigoureusement nulle en sortie. Cette tension est la tension de décalage, ou d'offset .
    
    Fig. 10. Erreur d'offset.
    En pratique, Analog Devices définit cette erreur comme étant l'écart entre la valeur théorique et la valeur réelle mesurée sur la première transition du convertisseur et exprimé en LSB. En pratique, pour ajuster un convertisseur, on réglera d'abord l'offset, et ensuite le gain.
  3. Erreurs de linéarité.
    
    L'erreur de linéarité est due au fait que la résolution des convertisseurs n'est pas constante.
    On distingue deux formes de non linéarité :
    - la non linéarité intégrale
    - la non linéarité différentielle
    la non linéarité intégrale , exprimée en LSB, est la différence maximum constatée sur toute la plage de conversion entre les valeurs théoriques et les valeurs mesurées.
    Cette mesure n'a évidemment de sens que si le zéro et le gain sont correctement réglés.
    La fonction de transfert est représentée figure 11.
    
    Fig. 11. Erreur de linéarité intégrale.
    La non linéarité différentielle concerne la différence de tension obtenue lors du passage au code numérique immédiatement supérieur ou inférieur ; théoriquement, cette valeur vaut 1 LSB. La non linéarité différentielle sera la différence entre l'écart mesuré et le LSB théorique. L'illustration est donnée en figure 12.
    
    Fig. 12. Erreur de linéarité différentielle.
    La valeur donnée dans les spécifications des constructeurs est la plus grande valeur constatée sur toute la plage de conversion.
    La non linéarité différentielle est plus gênante que la non linéarité intégrale, surtout dans le cas de mesures comparatives effectuées sur une faible partie de la plage de conversion.
    En général, et pour des causes technologiques bien identifiées, le maximum de non linéarité différentielle se trouve à la moitié de la pleine échelle (passage du MSB de 0 à 1), et ensuite à moindre degré à 1/4 et 3/4 de la pleine échelle.
    On sera donc vigilant quand on fera des mesures comparatives dans ces zones là.
  4. Monotonicité (CNA).
    
    Ce phénomène est le même que le précédent, mais poussé à l'extrême : il peut arriver que la pente de la courbe de conversion change de signe. Pour une tension analogique de sortie, il ne sera pas possible d'attribuer un nombre binaire correspondant : il y aura plusieurs solutions possibles.
    
    Fig. 13. Monotonicité.
  5. Codes manquants (CAN).
    
    Cette erreur pour le CAN est le pendant de la monotonicité pour le CNA.
    
    Fig. 14. Codes manquants
    Lors de la conversion, la courbe donnée binaire = f(tension analogique) n'étant pas une fonction (plusieurs codes binaires possibles pour une même tension d'entrée), le convertisseur choisira la plus faible valeur binaire parmi celles possibles. Les autres ne seront jamais utilisées, et formeront des " trous " dans le code binaire : ce sont les codes manquants.
  6. Temps d'établissement (CNA).
    
    Les étages de sortie des CNA sont généralement des amplificateurs opérationnels. On a vu que la tension de sortie va varier " par bonds " quand le code binaire d'entrée va changer. De ce fait, l'ampli de sortie va fonctionner en mode impulsionnel. La stabilisation de la tension de sortie n'est pas immédiate : elle peut être du type premier ordre ou oscillatoire amortie (deuxième ordre et plus).
    On appellera temps d'établissement (settling time en Anglais) le temps mis par la sortie pour atteindre un certain pourcentage de la tension finale stabilisée lorsque l'entrée va varier.
    
    Fig. 15. Temps d'établissement.
  7. Temps de conversion (CAN).
    
    Lorsqu'on numérise un signal, on envoie au CAN un ordre de conversion, et on récupère la valeur binaire en sortie au terme d'un délai appelé temps de conversion .
  8. Précision du convertisseur.
    
    Pour obtenir la précision globale du convertisseur, on cumulera toutes les erreurs précédemment citées.
    En général, ces erreurs sont données soit en % de la pleine échelle (% FS pour full scale), soit en fraction de quantum (± 1/2 LSB par exemple).
CONVERSION NUMÉRIQUE / ANALOGIQUE.

Il existe principalement deux types de convertisseurs numérique / analogique sur le marché : les convertisseurs à résistances pondérées, et les convertisseurs à réseau R/2R. Ces derniers sont prédominants.
Il existe aussi des convertisseurs à réseaux de condensateurs fonctionnant sur le même principe de base que les réseaux à résistances.
Nous n'exposerons pas ici les convertisseurs /, qui traitent non plus le code binaire absolu, mais la différence avec l'échantillon précédent. Ces convertisseurs sont très répandus dans l'audio-numérique (lecteurs de disques compacts), car ils sont précis et meilleur marché que les convertisseurs traditionnels. Pour l'instant, ils sont peu utilisés en mesure.
1. ARCHITECTURE GÉNÉRIQUE.
  
  Quel que soit le type de convertisseur étudié, on retrouvera toujours peu ou prou la même structure, constituée des même éléments de base ; seule la réalisation technologique des blocs de base différera d'un convertisseur à l'autre et en fera sa spécificité.
  Il est donc intéressant d'étudier l'architecture générique mettant en évidence les points communs à tous les convertisseurs.
  
  Fig. 16. Architecture des CNA.
  Sur la figure 16, on distingue 5 blocs :
  - un buffer numérique d'entrée : celui-ci est chargé de garder en mémoire la donnée numérique pendant le temps de conversion ; il sert aussi d'interface entre les parties numérique et analogique du convertisseur.
  - une référence de tension : son importance est capitale pour la précision de l'ensemble ; c'est elle qui donne le signal de référence servant à la détermination des tensions de sortie.
  - l'arbre de commutation (switching tree en anglais) : il est commandé par le buffer d'entrée et va déterminer les résistances qui seront alimentées par la référence de tension.
  - le réseau de résistances : c'est un ensemble de résistances, qui, alimentées par la référence de tension via l'arbre de commutation vont générer des courants très précis fonction du code binaire d'entrée.
  - le convertisseur courant/tension est un ampli servant à transformer les courants générés par le réseau de résistances en tension de sortie. Il est optionnel, certains CNA ne l'incluent pas, d'autres l'incluent, mais laissent le choix de l'utiliser ou non.
  On retrouvera donc toujours ces éléments de base, la distinction entre les convertisseurs se faisant généralement dans le réseau de résistances (et par voie de conséquences dans l'arbre de commutation).
2. CNA À RÉSISTANCES PONDÉRÉES.
  1. Principe.
    
    Le principe de fonctionnement de ce montage est extrêmement simple : il est basé sur un amplificateur opérationnel monté en sommateur inverseur.
    
    Fig. 17. Schéma de principe d'un CNA à résistances pondérées (4 bits).
    Les principaux constituants sont :
    - un amplificateur opérationnel.
    - une référence de tension qui va définir la pleine échelle du convertisseur.
    - une série de résistances dans un rapport des puissances successives de 2 (1, 2, 4, 8, 16...).
    - une série de registres numériques contenant le code binaire d'entrée.
    - des commutateurs analogiques (interrupteurs commandés électriquement par les signaux logiques) reliant les résistances à la référence de tension.
    Le schéma de la figure 17 montre un CNA 4 bits. Par extension, on peut construire un CNA ayant un nombre de bits quelconque en augmentant les entrées logiques et en y affectant des résistances de valeur convenable (toujours dans le rapport des puissances de deux).
    On remarque que le LSB est affecté à la résistance de plus grande valeur, et le MSB à celle de plus faible valeur.
    Nous appellerons a₀ le MSB, a₁ le bit suivant, ..., et a_N-1 le LSB d'un convertisseur à N bits.
    Si on applique le résultat de l'ampli sommateur inverseur à ce montage, on trouve :
    
    soit :
    
    Dans le cas de notre convertisseur 4 bits, la solution est :
    
    Le MSB est affecté du coefficient le plus fort, et les bits successifs voient leur coefficient divisé par deux par rapport au bit précédent.
    On peut calculer la résolution (LSB) de ce convertisseur : c'est la variation de la tension de sortie lorsque l'entrée numérique varie d'une unité, soit :
    
    Dans le cas général d'un convertisseur à N bits, on aurait :
    
    L'équation [2] va nous permettre de calculer la plage de conversion. Si on injecte le résultat de [7] dans l'équation [2], on obtient :
    
    où V_MAX représente la plage de conversion, ou pleine échelle du convertisseur. Pour notre convertisseur 4 bits, cette pleine échelle vaut donc 15/8^ème de E_ref. Ceci est dû au fait que le convertisseur de N bits comporte 2^N états différents, dont zéro , ce qui fait que le dernier état est égal à 2^N-1, et pas 2^N.
  2. Précision.
    
    Le schéma de ce convertisseur nous permet de mieux comprendre les erreurs citées au paragraphe précédent :
    - L'erreur de gain sera directement proportionnelle à l'imprécision de la référence de tension et de la résistance de contre-réaction.
    - L'erreur d'offset sera due à l'offset de l'amplificateur.
    - L'erreur de linéarité et la monotonicité seront dues au mauvais appairage des résistances dans le rapport des puissances de 2.
    - Le temps d'établissement sera donné par la réponse de l'amplificateur à un échelon de tension.
    Pour revenir aux erreurs de linéarité, il faut noter que la précision relative sur chaque résistance aura un impact sur le résultat global qui va doubler tous les bits en allant du LSB vers le MSB.
    En effet, une erreur de 10% de la résistance du LSB ne va fausser le résultat que de 1,1 fois le LSB.
    Par contre, 10% d'erreur sur la résistance du MSB va induire une erreur égale à 1,1 fois le MSB, soit 2^(N-1) fois plus que celle faite sur le LSB dans les mêmes conditions... Cette erreur peut facilement être supérieure au LSB et entraîner des non monotonicités dans la réponse (voir annexe).
  3. Avantages / inconvénients.
    
    L'avantage d'un tel montage est la simplicité. C'est un bon outil pédagogique.
    Malheureusement, la réalisation pratique est difficile du fait de la dynamique des résistances utilisées (2^N pour un convertisseur à N bits), et, on l'a vu, une tolérance nécessaire sur les résistance divisée par 2 à chaque bit supplémentaire. Pour un convertisseur à 8 bits, la précision de la résistance du MSB devra être meilleure que 1% pour être en limite de non monotonicité, et en pratique, on prendra une résistance à 2‰ au minimum.
    Le principal problème provient de l'intégration de ces résistances : dans les circuits intégrés, on sait tenir une telle précision, mais la proportionnalité des résistances est obtenues en leur donnant des dimensions proportionnelles à leur valeur. La dynamique élevée requise ici est vite prohibitive.
    Ces défauts font que ce convertisseur n'est pas viable économiquement, surtout si on le compare au CNA à réseau R/2R, plus facile à intégrer.
3. CNA À RÉSEAU R/2R.
  1. Principe
    
    Ce type de convertisseur prend en compte les défauts du précédent : il est bâti autour d'un réseau de résistances composé de seulement deux valeurs, R et 2R. Il n'y a donc plus le défaut inhérent à la grande dynamique de valeurs des résistances.
    
    Fig. 18. Schéma de principe d'un CNA à réseau R/2R (4 bits).
    Les composants sont sensiblement les mêmes que pour le CNA à résistances pondérées :
    - un amplificateur opérationnel.
    - une référence de tension qui va définir la pleine échelle du convertisseur.
    - un réseau de résistances R/2R.
    - une série de registres numériques contenant le code binaire d'entrée.
    - des commutateurs analogiques (interrupteurs commandés électriquement par les signaux logiques) reliant les résistances soit à la masse, soit à l'entrée - de l'ampli.
    L'amplificateur va fonctionner ici en convertisseur courant/tension : en fonction du positionnement des commutateurs, le courant total I_T sera plus ou moins élevé, et sera transformé en tension par l'ampli et la résistance de contre-réaction. Certains CNA offrent d'ailleurs simplement une sortie en courant, et c'est à l'utilisateur de l'utiliser tel quel, ou de le convertir en tension.
    Avant d'attaquer la mise en équation, nous allons faire un constat, et partant de là, étudier certaines propriétés du réseau R/2R.
    L'entrée + de l'ampli est à la masse ; si on considère que cet ampli est parfait, l'entrée - est au même potentiel, soit 0 masse virtuelle). La position du commutateur n'influe donc nullement sur le fonctionnement du réseau : les courants I₀ à I₃ sont dirigés soit vers le convertisseur courant/tension, soit dérivés à la masse, mais le potentiel à la borne commune des commutateurs reste le même, à savoir 0.
    Pour simplifier le raisonnement, nous allons donc étudier le réseau suivant :
    
    Fig. 19. Réseau R/2R.
    Les courants I₃ et I_D sont égaux (diviseur de courant avec deux résistances égales).
    On a donc :
    
    Les branches où circulent I₃ et I_D sont en fait deux résistances égales (2R) en parallèle, soit l'équivalent d'une résistance moitié, donc R. Cette résistance équivalente est en série avec celle où circule I_C. Le courant I_C circule donc dans une résistance équivalent à 2R. Le circuit devient :
    
    Fig. 20. Réseau réduit équivalent.
    On retombe strictement sur le même type de réseau que précédemment. On en déduit facilement :
    
    L'étape finale du raisonnement donne le réseau suivant :
    
    Fig. 21. Réseau final.
    On en déduit la valeur des courants :
    
    Le réseau R/2R nous fournit des courant en progression géométrique de raison 2 : on retombe sur la même chose que le convertisseur à résistances pondérées.
    La tension de sortie V_s du convertisseur sera égale à :
    
    Le résultat est donc du même genre que pour le CNA à résistances pondérées. On note un facteur 1/4, mais on peut remarquer qu'il suffit de mettre une résistance égale à 4R en contre-réaction pour retomber sur le même résultat.
  2. Précision.
    
    Pour ce qui est de la précision requise sur les résistances, on retrouve les mêmes défauts que pour le CNA précédent :
    - la référence de tension et la résistance de contre-réaction vont engendrer la même erreur de pleine échelle.
    - une erreur sur la résistance du MSB aura 2^(N-1) fois plus d'influence que la même erreur sur le LSB.
    Par contre, l'intégration sera plus aisée, et on sera capables de faire des convertisseurs précis et à plus grand nombre de bits que le CNA à résistances pondérées.
    En instrumentation, on rencontrera fréquemment des CNA à 12bits de ce type, notamment sur des cartes d'acquisition de données pour micro-ordinateurs.
    La structure du réseau et des commutateurs autorise une vitesse de conversion assez grande, car lors du basculement du commutateur, les résistances restent au même potentiel : il n'y a donc pas d'influence des inévitables capacités parasites qui mettraient du temps à se charger et à se décharger à travers les résistances. Ceci autorise l'utilisation de résistances d'assez grande valeur, ce qui limite l'erreur due aux résistances à l'état passant des commutateurs (quelques dizaines à quelques centaines d'ohms).
4. UTILISATION DES CNA.
  - Utilisation " classique "
    
    Les CNA sont bien entendu utilisables tels quels pour faire de la conversion numérique/analogique.
    On les retrouvera en sortie de chaîne de traitement numérique lorsqu'un signal analogique est requis (commande d'un transducteur, contrôle de processus...
    Ils seront suivis d'un filtre plus ou moins sophistiqué destiné à supprimer les " marches d'escalier " inhérentes à la numérisation. Dans le cas de l'audio numérique, le filtrage est d'une importance fondamentale, et c'est lui qui conditionne grandement la qualité du son. Cet aspect n'est donc pas à sous estimer.
    Il faudra faire attention au filtrage dans le cas où ces convertisseurs sont inclus dans une boucle d'asservissement : les escaliers peuvent être néfaste à la stabilité du système.
  - Amplificateurs à gain programmable.
    
    Les montages étudiés peuvent se résumer tous les deux à une chose : ce sont des amplificateurs d'une tension continue (E_ref) dont le gain est ajustable par une entrée numérique (les codes binaires).
    On peut donc penser à une autre utilisation des CNA : si on remplace E_ref par une tension alternative quelconque, on peut utiliser l'entrée numérique pour faire varier le gain de l'ampli, et donc le signal en sortie.
    Cette application ouvre la porte aux VCA (voltage controlled amplifier), atténuateurs à commande numérique (donc télécommandables à distance)...
  - Filtres programmable
    
    De la même manière, on peut intégrer ces réseaux dans certains schémas de filtres, et obtenir ainsi des filtres à fréquence de coupure variable et commandée par un signal numérique.
  - Multiplieur.
    
    Une autre application importante est la multiplication de signaux : l'un sera analogique (en remplacement de E_ref), et l'autre numérique. Ce signal numérique pourra être un signal préalablement numérisé. La sortie va donner le produit des deux signaux.
  - Attention !!!
    
    Toutes ces applications " spéciales " ne peuvent marcher que s'il est possible d'appliquer des tensions bipolaires sur l'entrée E_ref. Il faut donc pouvoir alimenter symétriquement le montage, et les commutateurs analogiques doivent être bidirectionnels, ce qui n'est pas toujours le cas. On peut toujours polariser le signal pour qu'il soit globalement unipolaire, mais ces applications perdent de leur intérêt : la tension de polarisation étant traitée comme le signal, il sera difficile de l'extraire en sortie du convertisseur.
    Les fabricants de convertisseurs indiquent si leurs produits sont conçus pour fonctionner dans ces applications " dérivées ". Il faudra donc se reporter à leur documentation.
CONVERSION ANALOGIQUE / NUMÉRIQUE.

Parmi les principes de conversion analogique / numérique disponibles, nous en avons choisis trois particulièrement représentatifs, et qui se différencient très nettement en terme de compromis vitesse / précision :
- les convertisseurs parallèles (ou flash en Anglais), très rapides, mais limités en précision. Leur rapidité les destine en particulier aux oscilloscopes numériques, qui se contentent de convertisseurs à 6 ou 8 bits.
- les convertisseurs à approximations successives , moins rapides que les précédents, mais avec des possibilités en résolution bien supérieures (8 à 16 bits). Ils couvrent un vaste champ d'applications en mesure, de la carte d'acquisition de données pour micro ordinateur aux CAN intégrés dans des micro contrôleurs qui servent à piloter les applications les plus variées...
- les convertisseurs à comptage d'impulsion sont très précis, et par construction, sont aptes à filtrer des bruits importants. En contrepartie, ils sont très lents, donc destinés à faire des mesures de signaux stabilisés.
1. ARCHITECTURE GÉNÉRIQUE.
  
  Comme pour le CNA, il peut être intéressant de voir les points communs aux CAN de technologies différentes (hors convertisseurs à rampe).
  
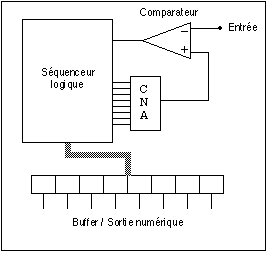
  Fig. 22. Architecture d'un CAN
  La pièce centrale du schéma de la figure 22 est... un CNA !
  En pratique, un séquenceur logique va balayer les codes binaires (de façon plus ou moins astucieuse), ces codes vont être convertis en une tension analogique par le CNA, tension qui va être comparée à celle d'entrée. Le basculement du comparateur arrête le processus, et la donnée est basculée et mémorisée dans le buffer de sortie.
  Il ne faut pas oublier ce que cache ce schéma, à savoir la composition du CNA, et en particulier la référence de tension. Cette référence peut d'ailleurs être intégrée ou non dans le CAN ; dans ce dernier cas, il faudra en mettre une à l'extérieur (la remarque est valable pour les CNA).
2. CAN PARALLÈLE.
  1. Principe.
    
    La tension à mesurer est comparée simultanément à 2^N-1 tensions de référence, N étant le nombre de bits du convertisseur. Le nombre 2^N-1 s'explique par la notion de pleine échelle vue précédemment : 0 est l'état logique supplémentaire qui fait 2^N états au total pour un convertisseur à N bits.
    Ce convertisseur est composé des éléments suivants :
    - une tension de référence E_ref.
    - un réseau de 2^N résistances montées en série. Elles ont la même valeur R à l'exception notable de la première et de la dernière qui ont la valeur 3R/2 et R/2 : c'est l'astuce qui permet de faire basculer le premier comparateur non pas lorsque la tension d'entrée est égale à 1 LSB, mais 1/2 LSB. Au lieu d'avoir une erreur maxi de 1LSB (toujours par défaut), on aura une erreur de ±1/2 LSB (par excès ou par défaut) : voir plus haut. La dernière résistance vaut 3R/2 pour équilibrer le réseau, et pour que le LSB soit conforme à sa valeur donnée dans l'équation [1].
    - 2^N-1 comparateurs comparent en permanence la tension à mesurer à une des tensions de référence délivrée par le pont de résistances.
    - un décodeur logique permet de traduire l'état des comparateurs en code binaire de sortie.
    
    Fig. 23. CAN parallèle à 3 bits.
  2. Précision.
    
    Dans le principe, ce CAN pourrait être relativement précis. En pratique, on butte sur un inconvénient de taille : il faut 2^N-1 comparateurs pour un convertisseur à N bits, soit 63 comparateurs pour un 6 bits et 255 pour un 8 bits ! Le procédé devient donc vite limitatif.
    La principale source d'erreur provient de l'offset des comparateurs qui va introduire de la non linéarité différentielle.
    La rapidité va être conditionnée par la vitesse des comparateurs et du décodeur logique. La cadence de conversion est nettement supérieure au MHz, et peut atteindre des centaines de MHz pour les oscilloscopes numériques.
  3. Utilisation.
    
    De par leur principe, ces CAN sont limités à 6 ou 8 bits, ce qui est insuffisant pour de l'instrumentation.
    Ce handicap est négligeable en oscilloscopie numérique : certains constructeurs utilisent des convertisseurs 6 bits, ce qui est suffisant pour décrire l'axe vertical de l'écran avec une résolution supérieure à 2%.
    Pour les applications requérant des vitesses élevées mais non extrêmes, on utilise des convertisseurs semi-parallèles, qui utilisent beaucoup moins de comparateurs et conservent une vitesse de conversion intéressante, ceci avec une résolution pouvant atteindre 12 bits.
3. CAN À APPROXIMATIONS SUCCESSIVES.
  
  Ces convertisseurs sont très répandus car performants et bon marché (tout est relatif quand même !).
  1. Principe.
    
    Un schéma de principe est donné figure 24. On y trouve principalement une référence de tension, un CNA, un comparateur et un séquenceur logique piloté par horloge.
    Le séquenceur logique délivre un code binaire à l'entrée du CNA. La tension de sortie de ce CNA est comparée à la tension à mesurer, et en fonction du résultat, le code binaire est modifié de manière à approcher la valeur à trouver.
    L'exemple le plus simple de séquenceur logique est un compteur binaire qui s'incrémente d'une unité à chaque coup d'horloge (montage vu en TP). Tous les codes binaires sont successivement comparés à la tension d'entrée. Quand le signal de sortie du comparateur s'inverse, la tension de référence vient juste de dépasser la valeur à mesurer : la conversion est terminée, il ne reste qu'à lire la valeur binaire (donnée ici par excès).
    
    Fig. 24. CAN à approximations successives.
    Ce séquenceur ne présente en pratique aucun intérêt, si ce n'est l'aspect pédagogique. Pour un convertisseur 12bits, il faudrait entre 0 et 4095 coups d'horloge : le temps de conversion ne serait pas constant, et surtout, serait beaucoup trop long pour les fortes valeurs de tension d'entrée.
    Les décodeurs fonctionnent en fait sur le principe de la dichotomie (figure 25) :
    - on compare d'abord la tension à mesurer E_x à une tension de référence correspondant à tous les bits à 0 sauf le MSB à 1 (étape 1). Si cette tension de référence est inférieure à E_x, on laisse le MSB à 1, sinon, on le positionne à 0.
    - tout en laissant le MSB dans l'état déterminé précédemment, on fixe le bit suivant à 1 et on applique le mode opératoire précédent (étape 2).
    - on procède ainsi de bit en bit, N fois pour un convertisseur à N bits
    La conversion est faite rapidement, et le temps de conversion est le même quelle que soit la tension d'entrée.
    
    Fig. 25. Approximations par dichotomie.
    Un exemple plus concret est donné à la figure 26 (principe de base réduit à 3 bits des ADC 800 et dérivés de chez National Semi-conducteurs).
    
    Fig. 26. Exemple de CAN à approximations successives.
    On retrouve le réseau de résistances du convertisseur parallèle de la figure 23, mais chaque nœud de ce réseau est connecté non pas à un comparateur, mais à un réseau de commutateurs de connection (switching tree) dont le point final est relié à l'entrée d'un comparateur ; l'autre entrée de ce comparateur est reliée à la tension à mesurer E_x.
    Chaque sortie logique du séquenceur actionne simultanément tous les commutateurs de même niveau (situés sur la même verticale sur le schéma).
    Sur le schéma, a₂a₁a₀ est égal à la valeur binaire 101, soit 5. Si on suit le chemin des commutateurs fermés, on tombe bien sur la référence de tension correspondant à la valeur logique 5, soit 101 en binaire.
    En appliquant la règle de séquencement précédente, on trouve le code logique en 3 approximations (CAN à 3 bits).
    N.B : l'ensemble composé du réseau de résistances et des commutateurs est bien un CNA : il suffit de relier le point de sortie du réseau de connexion à un ampli suiveur pour avoir un type de CNA non étudié dans le paragraphe précédent mais parfaitement viable ! Il est seulement coûteux en résistances et en commutateurs si on le compare aux CNA à réseau R/2R ou à résistances pondérées.
  2. Précision.
    
    Ces convertisseurs sont précis : il suffit d'un bon comparateur associé à un CNA de la résolution voulue pour obtenir la précision désirée.
    La rapidité sera limitée par le temps d'établissement du CNA, la vitesse de réaction du comparateur, et la complexité de la logique.
    Les convertisseurs 12 bits courants (qui sont beaucoup utilisés en instrumentation) ont un temps de conversion de l'ordre de 10 à 200µs, ce qui fait des cadences d'échantillonnage comprises entre 5 et 100kHz environ.
    Important : la conversion prend un certain temps ; de plus, vu le principe utilisé, la comparaison ne se fait pas avec des codes binaires successifs. Il est impératif dans ce cas de figer la tension d'entrée pendant la conversion .
    Cette fonction va être réalisée par un échantillonneur / bloqueur (E/B) : lorsque l'ordre de conversion est donné par le séquenceur logique, la sortie de l'E/B prend la valeur courante du signal et se fige à cette valeur (effet mémoire).
    L'E/B est nécessaire pour éviter des codes manquants et/ou des erreurs de conversion. Il est parfois intégré dans le CAN. Si ce n'est pas le cas, on le placera entre le signal à mesurer et le CAN.
    Il faudra veiller à ce que sa précision (offset, erreur de gain) soit compatible avec le CAN placé en aval : inutile de mettre un CAN 16 bits ultra précis derrière un E/B de deuxième catégorie...
    De même, on fera attention au temps d'établissement de ce composant.
  3. Utilisation.
    
    On retrouve ces composants un peu partout, de l'audio numérique aux cartes d'acquisition de données en passant par l'intégration dans des micro contrôleurs.
    Comme les convertisseurs parallèles, ils mesurent des valeurs instantanées d'un signal ; il faudra donc s'assurer que celui-ci est exempt de bruit (du moins dans la limite de la résolution du CAN).
    Cette fonction sera assurée par un câblage correct de la chaîne de mesure, et un filtrage avant acquisition (attention à la fréquence de cassure du filtre qui servira par la même occasion de filtre anti-repliement --loi de Shannon).
4. CAN À COMPTAGE D'IMPULSIONS.
  
  Cette catégorie de convertisseur est très répandue : tous les multimètres " de poche " fonctionnent sur ce principe. Ils offrent une grande précision pour un faible coût, mais de par leur principe, ils ne peuvent mesurer que des tensions statiques ou faire des moyennes, contrairement aux convertisseurs précédents qui échantillonnent le signal instantané.
  On trouve 4 types de convertisseurs à rampe (de simple à quadruple rampe : le principe reste globalement le même, les rampes supplémentaires venant compenser diverses erreurs), ainsi que des convertisseurs tension-fréquence.
  Tous ces convertisseurs sont basés sur une opération de chronométrage (comptage d'impulsions) pendant un temps proportionnel à la tension d'entrée.
  1. Convertisseur simple rampe.
    
    Fig. 27. Convertisseur simple rampe.
    Le schéma de principe d'un tel convertisseur est donné figure 27. Les principaux éléments le constituant sont :
    - un générateur de rampe (intégration d'une tension de référence).
    - deux comparateurs comparant la rampe l'un au zéro, l'autre à la tension à mesurer.
    - divers éléments de logique, dont un générateur de porte, une horloge, un compteur et un système d'affichage.
    Lorsque la logique commande le démarrage d'une mesure, il y a remise à zéro de l'intégrateur (rampe) et des compteurs ; ensuite, la tension de rampe croît linéairement avec le temps (figure 28).
    Quand le premier comparateur bascule à t₀, la porte autorise le comptage des impulsions délivrées par l'horloge.
    Quand le deuxième comparateur bascule, il ferme cette porte, et la valeur contenue dans les compteurs est verrouillée et transmise aux afficheurs.
    
    Fig. 28. Tension en sortie d'intégrateur et porte.
    On a donc fait un chronométrage des impulsions de l'horloge pendant un temps proportionnel à la tension à mesurer.
    Cette tension est égale à :
    
    Si N est le nombre d'impulsions comptées et F la fréquence de l'horloge, on a :
    
    La pleine échelle sera donnée en nombre de points N_max, c'est à dire le comptage maximum autorisé par la dynamique des compteurs. Dans ce cas, la résolution sera l'inverse de N_max, et elle sera d'autant meilleure que N_max sera grand.
    Le résultat montre qu'on aura intérêt à avoir une fréquence d'horloge élevée à rampe donnée pour avoir une bonne résolution.
    Il indique aussi le plus gros défaut de ce convertisseur : la mesure dépend de la fréquence d'horloge, de la tension de référence, et des composants R et C de l'intégrateur.
    Si on sait faire des horloges à quartz stables et des références de tension de précision, il en est tout autrement avec les capacités servant dans l'intégrateur : la précision initiale est moyenne (sauf tri), et les dérives (vieillissement, température...) difficiles à maîtriser.
    L'autre gros défaut est une grande sensibilité au bruit : si la tension d'entrée varie sous l'effet d'une perturbation quelconque, le deuxième comparateur peut fermer la porte et arrêter le processus de comptage : la valeur lue sera fausse.
    Il faut noter ici que la tension d'entrée doit impérativement être fixe , sinon, on mesure n'importe quoi !
    Comme le comptage dure un certain temps, on voit que toutes ces conditions sont difficiles à réunir.
  2. Convertisseur double rampe.
    
    Ce type de convertisseur va pallier les défauts du simple rampe. Le schéma de principe est le suivant :
    
    Fig. 29. Schéma de principe du convertisseur double rampe.
    
    Fig. 30. Tension en sortie d'intégrateur.
    La mesure se fait en deux temps :
    - l'intégrateur ayant été remis à zéro, on commute son entrée sur la tension à mesurer. Le comptage démarre.
    - quand il atteint un nombre N₁ déterminé, on commute l'entrée de l'intégrateur sur une tension de référence E_ref de polarité opposée à E_x. On compte les impulsions d'horloge jusqu'à ce que la tension de sortie de l'intégrateur s'annule, soit N₂.
    Si F est la fréquence de l'horloge, on peut écrire :
    
    La valeur affichée est directement proportionnelle au comptage, et elle est indépendante des composants R et C, et aussi de la fréquence de l'horloge. On pourrait comparer cette méthode à la double pesée avec une balance...
    L'autre gros avantage du montage double rampe est son immunité au bruit : le signal étant intégré, seule la valeur moyenne du bruit sera prise en compte, soit une valeur nulle dans la plupart des cas. Si un parasite perturbe le signal lors de la mesure, seule son intégrale sera prise en compte ; s'il est bref, elle sera négligeable, et le résultat très peu modifié.
  3. Résolution. Précision.
    
    Pour ce type de convertisseurs, la dynamique n'est plus exprimée en bits, mais en points, qui correspondent à la capacité maximum du compteur.
    Les multimètres de poche font 2000 ou 3000 points, les plus évolués en font 20 000 ou 30 000, et les multimètres de laboratoire dépassent allégrement les 100 000 points.
    Il ne faut toutefois pas se leurrer quand à leur précision réelle, qui est souvent bien en deçà de la résolution.
    Par exemple, un multimètre 2000 points (11 bits équivalent à 2048 points) ne dépasse guère une précision de 0,5% de pleine échelle, soit l'équivalent de 8bits ! Et encore, ceci est valable pour des mesures de tensions continues ; pour les mesures de courant ou de résistances, la précision peut tomber à 1 ou 2%. En fait, ce sont les composants externes au convertisseur (ampli, atténuateur) qui déterminent la précision.
    Il faudra donc bien se garder de prendre pour argent comptant la valeur de l'affichage, et se rappeler que (au moins) le digit le moins significatif est faux. Dans tous les cas, il faut consulter la spécification de l'appareil pour connaître sa précision réelle, et ne pas se laisser impressionner par l'affichage...

[ Table des mati�res ]