Bragg's Law and Diffraction:
How waves reveal the atomic structure of crystals

What is Bragg's Law and Why is it Important?

Bragg's Law refers to the simple equation:

nl = 2d sinq (1)

derived by the English physicists Sir W.H. Bragg and his son Sir W.L. Bragg in 1913 to explain why the cleavage faces of crystals appear to reflect X-ray beams at certain angles of incidence (theta, q). The variable d is the distance between atomic layers in a crystal, and the variable lambda l is the wavelength of the incident X-ray beam (see applet); n is an integer

This observation is an example of X-ray wave interference (Roentgenstrahlinterferenzen), commonly known as X-ray diffraction (XRD), and was direct evidence for the periodic atomic structure of crystals postulated for several centuries. The Braggs were awarded the Nobel Prize in physics in 1915 for their work in determining crystal structures beginning with NaCl, ZnS and diamond. Although Bragg's law was used to explain the interference pattern of X-rays scattered by crystals, diffraction has been developed to study the structure of all states of matter with any beam, e.g., ions, electrons, neutrons, and protons, with a wavelength similar to the distance between the atomic or molecular structures of interest.

How to Use this Applet

The applet shows two rays incident on two atomic layers of a crystal, e.g., atoms, ions, and molecules, separated by the distance d. The layers look like rows because the layers are projected onto two dimensions and your view is parallel to the layers. The applet begins with the scattered rays in phase and interferring constructively. Bragg's Law is satisfied and diffraction is occurring. The meter indicates how well the phases of the two rays match. The small light on the meter is green when Bragg's equation is satisfied and red when it is not satisfied.

The meter can be observed while the three variables in Bragg's are changed by clicking on the scroll-bar arrows and by typing the values in the boxes. The d and q variables can be changed by dragging on the arrows provided on the crystal layers and scattered beam, respectively.

Deriving Bragg's Law

Bragg's Law can easily be derived by considering the conditions necessary to make the phases of the beams coincide when the incident angle equals and reflecting angle. The rays of the incident beam are always in phase and parallel up to the point at which the top beam strikes the top layer at atom z (Fig. 1). The second beam continues to the next layer where it is scattered by atom B. The second beam must travel the extra distance AB + BC if the two beams are to continue traveling adjacent and parallel. This extra distance must be an integral (n) multiple of the wavelength (l) for the phases of the two beams to be the same:

nl = AB +BC (2).

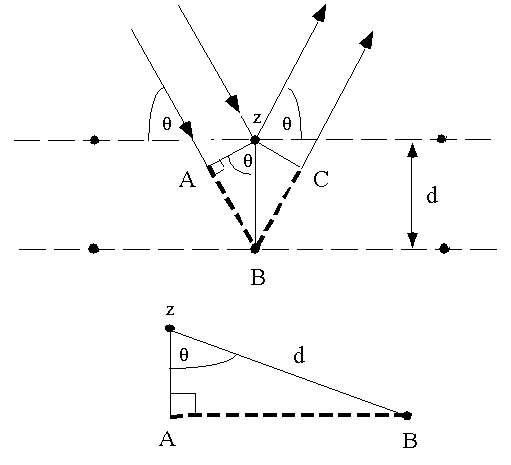
Fig. 1 Deriving Bragg's Law using the reflection geometry and applying trigonometry. The lower beam must travel the extra distance (AB + BC) to continue traveling parallel and adjacent to the top beam.

Recognizing d as the hypotenuse of the right triangle Abz, we can use trigonometry to relate d and q to the distance (AB + BC). The distance AB is opposite q so,

AB = d sinq (3).

Because AB = BC eq. (2) becomes,

nl = 2AB (4)

Substituting eq. (3) in eq. (4) we have,

nl = 2 d sinq, (1)

and Bragg's Law has been derived. The location of the surface does not change the derivation of Bragg's Law.

Experimental Diffraction Patterns

The following figures show experimental x-ray diffraction patterns of cubic SiC using synchrotron radiation.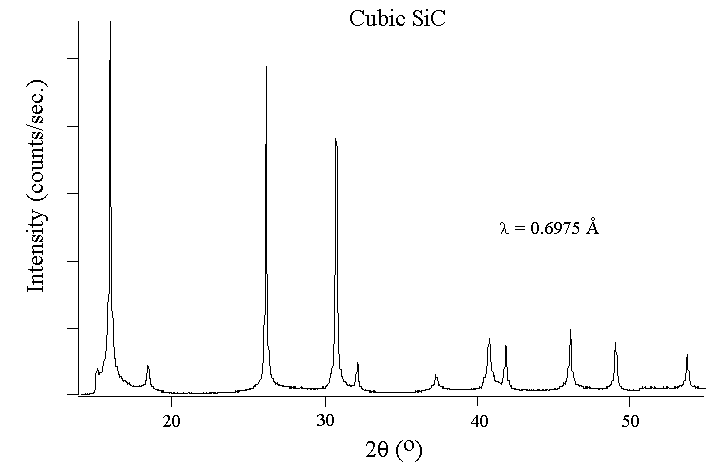

Players in the Discovery of X-ray Diffraction

Friedrich and Knipping first observed Roentgenstrahlinterferenzen in 1912 after a hint from their research advisor, Max von Laue, at the University of Munich. Bragg's Law greatly simplified von Laue's description of X-ray interference. The Braggs used crystals in the reflection geometry to analyze the intensity and wavelengths of X-rays (spectra) generated by different materials. Their apparatus for characterizing X-ray spectra was the Bragg spectrometer.

Laue knew that X-rays had wavelengths on the order of 1 Å. After learning that Paul Ewald's optical theories had approximated the distance between atoms in a crystal by the same length, Laue postulated that X-rays would diffract, by analogy to the diffraction of light from small periodic scratches drawn on a solid surface (an optical diffraction grating). In 1918 Ewald constructed a theory, in a form similar to his optical theory, quantitatively explaining the fundamental physical interactions associated with XRD. Elements of Ewald's eloquent theory continue to be useful for many applications in physics.

Do We Have Diamonds?

If we use X-rays with a wavelength (l) of 1.54Å, and we have diamonds in the material we are testing, we will find peaks on our X-ray pattern at q values that correspond to each of the d-spacings that characterize diamond. These d-spacings are 1.075Å, 1.261Å, and 2.06Å. To discover where to expect peaks if diamond is present, you can set l to 1.54Å in the applet, and set distance to one of the d-spacings. Then start with q at 6 degrees, and vary it until you find a Bragg's condition. Do the same with each of the remaining d-spacings. Remember that in the applet, you are varying q, while on the X-ray pattern printout, the angles are given as 2q. Consequently, when the applet indicates a Bragg's condition at a particular angle, you must multiply that angle by 2 to locate the angle on the X-ray pattern printout where you would expect a peak.