Etant donné le schéma de régulation de la figure, on désire trouver les polynômes
de manière à obtenir en boucle fermée un modèle
imposé.
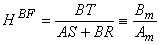
La résolution de l'équation diophantine (ou identité de Bezout)
conduit à l'identification des polynômes S et R. Les
polynômes R et S jouent un rôle en régulation, tandis que T
assure la poursuite.
T est déterminé afin que
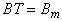
Contraintes sur les degrés des polynômes
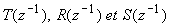
- pour assurer la réalisabilité (contrainte de
causalité)
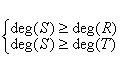
- pour une solution unique de l'identité de Bezout
L'identité de Bezout possède une solution unique minimale (les degrés des polynômes R et S sont les plus petites possibles) pour:
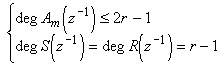
où
- il n'y a pas de restriction sur les degrés des polynômes A et
B de la fonction de transfert du procédé.
- il n'y a pas de restriction sur le retard du procédé
- il n'y a pas de restriction sur les zéros du procédé, car la méthode ne les compense pas; ils peuvent être stables ou instables