Détermination du coefficient d'amortissement d'un système discret à partir du lieu de ses pôles

Par analogie avec le cas continu, on peut déterminer à partir du plan des pôles en z le coefficient d'amortissement d'un système du deuxième ordre, possédant une paire de pôles complexes conjugués.

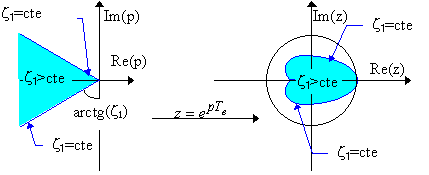
Les droites de pente constante 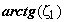, dans le plan des pôles en p, se transforment dans le plan des pôles en z, en spirales logarithmiques.

Imposer à un système discret un amortissement suffisamment important, revient à placer ses pôles à l'intérieur d'une spirale logarithmique définie par le seuil supérieur d'amortissement désiré.