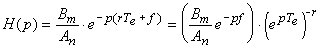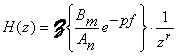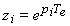Pour calculer la fonction de transfert discrète d'un système
continu dont la sortie est échantillonnée et dont l'entrée
est échantillonnée, on peut utiliser la transformée en
z:
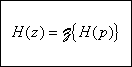
Des tables des transformées en z sont disponibles pour faciliter les
calculs.
Si la fonction de transfert du système continu possédant un
retard pur
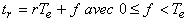 est
est
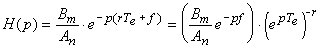
alors, la fonction de transfert échantillonnée par conservation
de la réponse impulsionnelle sera:
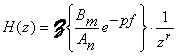
Remarques:
- Dans le cas où le système continu ne possède
pas de retard pur
- l'ordre du système est conservé
- il y a n pôles qui peuvent être calculés à
partir des pôles du système continu pi par
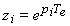
- quel que soit le nombre de zéros en continu, le nombre de
zéros en discret est n-1 (ou n), selon la valeur initiale nulle(ou
non-nulle) de la réponse impulsionnelle.
- le gain statique n'est pas conservé
- Dans le cas où le système continu possède un retard
pur, r pôles à l'origine vont s'ajouter au dénominateur de
la fonction de transfert échantillonné. Il y a également
un ajout de zéros si le retard fractionnaire est non-nul. L'ordre du
système va augmenter avec la valeur du retard pur multiple de la
période d'échantillonnage
[ Table des matières ]

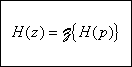
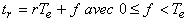 est
est