Soit un système continu d'ordre n possédant un retard pur
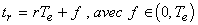 et r entier
et r entier
et de fonction de transfert
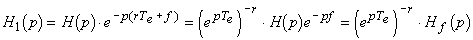
où r est appelé retard pur multiple de la période
d'échantillonnage et f retard fractionnaire.
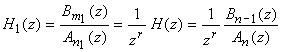
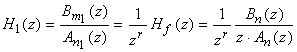
Remarques
- Quel que soit le nombre de zéros du système continu, la
fonction de transfert échantillonnée en présence du
bloqueur d'ordre zéro possède n-1 zéros, dans le cas sans
retard fractionnaire, et n zéros s'il existe un retard fractionnaire.
- L'ordre du système est conservé lors de
l'échantillonnage lorsque le système continu ne possède
pas de retard pur. Si le système continu possède un retard pur,
l'ordre du système échantillonné augmente avec la
diminution de la période d'échantillonnage.
- Un retard pur multiple de la période d'échantillonnage en
continu se transforme en échantillonné en r pôles à
l'origine.
Attention !
La présence de r pôles à l'origine ne signifie pas
nécessairement qu'il existe un retard en continu. Par exemple, le
dérivateur idéal continu de fonction de transfert H(p)=p se transforme en
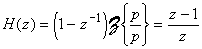 qui possède un pôle à l'origine.
qui possède un pôle à l'origine.
[ Table des matières ]
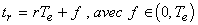 et r entier
et r entier
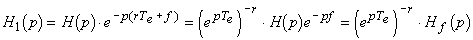
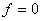
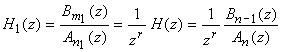
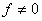
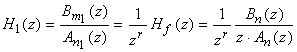
 qui possède un pôle à l'origine.
qui possède un pôle à l'origine.