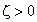Influence du coefficient d’amortissement sur la stabilité d’un système

Par analogie avec le cas continu, on déduit:

	Un système du deuxième ordre est *asymptotiquement stable* lorsque son coefficient d'amortissement prend des valeurs strictement positives.
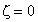	Le système est *à la limite de stabilité*. Les oscillations ne s'atténuent pas et il n'y a pas de convergence, même si la sortie reste bornée.
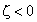	Le système est *instable*.