Détermination du retard pur sur la fonction de transfert

Cas d'un système numérique

Sur la forme standard (polynomiale ou pôles/zéros) de la fonction de transfert d'un système numérique,



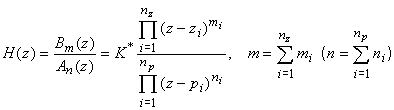
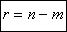
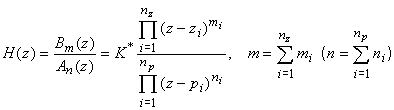
on calcule le retard pur (multiple de la période d'échantillonnage) par la formule:

Cas d'un système échantillonné

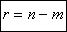
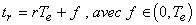Soit un système continu possédant un retard et de fonction de transfert



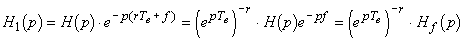
où

• r est appelé retard pur multiple de la période d'échantillonnage et

• f retard fractionnaire.

Par échantillonnage, on obtient une fonction de transfert en z



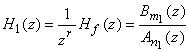
Si 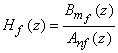et 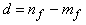est l'excès de pôles, alors on peut retrouver le retard pur multiple de la période d'échantillonnage du système continu par la formule:

Dans le cas d'un système strictement propre échantillonné précédé par un bloqueur d'ordre zéro l'excès de pôles d est toujours égal à 1. Le retard pur multiple de la période d'échantillonnage du système continu est

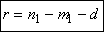
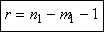
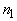où est le degré du polynôme dénominateur de la fonction de transfert du système échantillonné et 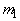est le degré du polynôme numérateur.

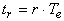La présence de r pôles à l'origine ne signifie pas nécessairement qu'il existe un retard en continu. Par exemple, le dérivateur idéal continu de fonction de transfert H(p)=p se transforme en 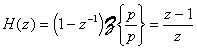qui possède un pôle à l'origine.