Transposition des zéros continus en échantillonné lors de la conversion d'une fonction de transfert continue en fonction de transfert discrète par une méthode rigoureuse
La transformée 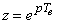 utilisée pour la transposition
des pôles en échantillonné est justifiée par la correspondance qui existe entre les
modes à temps continu et à temps discret. Au pôle p=pi, correspond une réponse
de la forme
utilisée pour la transposition
des pôles en échantillonné est justifiée par la correspondance qui existe entre les
modes à temps continu et à temps discret. Au pôle p=pi, correspond une réponse
de la forme 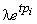 . Cette même réponse, échantillonnée,
donne
. Cette même réponse, échantillonnée,
donne 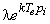 , que l'on peut associer à un pôle
de la forme
, que l'on peut associer à un pôle
de la forme 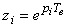 .
.
Cette substitution n'a aucune justification pour les zéros de la fonction de transfert.
On notera en particulier qu'un système associé à un bloqueur d'ordre zéro contient après échantillonnage un nombre de zéro plus élevé qu'en continu (en général n-1 s'il est d'ordre n).
On parle en échantillonné de système à non minimum de phase pour des systèmes à zéros à l'extérieur du cercle unité, bien que ce soit un abus de langage. Il vaut mieux dire système à inverse instable. Un système continu à inverse stable (respectivement instable) peut devenir en échantillonné à inverse instable (respectivement stable).