Démonstration

Soit l'intégrale 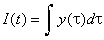. Sa transformée de Laplace est

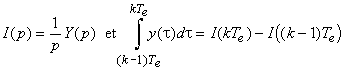
Si l'intégrale sur cet intervalle peut être exprimée linéairement en fonction des échantillons de y(t), alors la transformée en z peut être appliquée à cette expression:

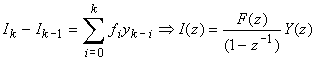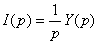. Comme , il est possible de faire l'approximation .
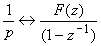