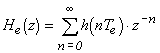La transformée en z: méthode rigoureuse de transposition d'une fonction de transfert continue en discret, par conservation de la réponse impulsionnelle

Définition

La transposition d'une fonction de transfert continue en fonction de transfert discrète par conservation de la réponse impulsionnelle est réalisée à l'aide de la transformée en z.

La transformée en z d'un signal discret 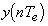est définie par la série des puissances négatives suivante, où z est une variable formelle complexe:

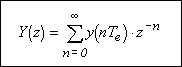
La transformée en z est calculée comme la transformée de Laplace d'un train d'impulsions (échantillonnage idéal) avec un changement de notation

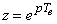
Soit la réponse impulsionnelle h(t), d'un système continu de fonction de transfert H(p). Alors, l'échantillonnée de h(t) est

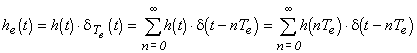
La transformée de Laplace du signal échantillonné est:

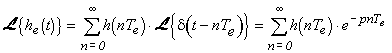
Avec le changement de notation 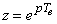, on obtient