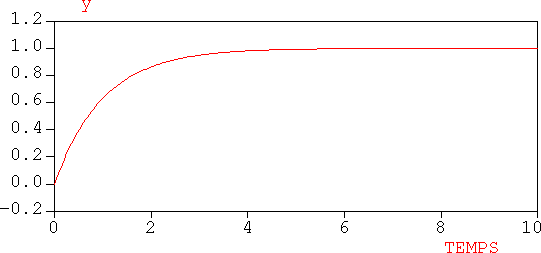
Les systèmes du premier ordre sont toujours apériodiques.

Les systèmes du premier ordre sont toujours apériodiques.
Soit la fonction de transfert du deuxième ordre :
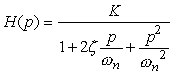
et l'entrée :
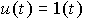 ,
,
z > 0.
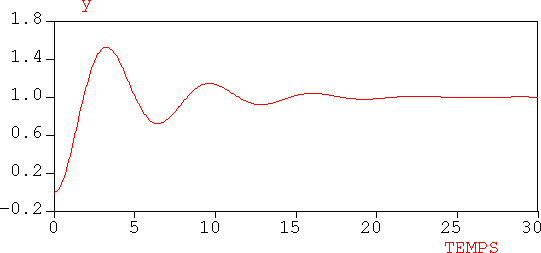
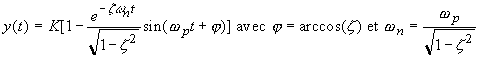
On remarque que y(0)=0 et
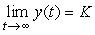 .
.
La courbe y(t) part donc de l'origine avec une tangente horizontale; elle tend vers l'asymptote y=K suivant un régime oscillatoire amorti. y(t) est le produit d'une fonction sinusoïdale du temps par une exponentielle décroissante. Les oscillations ne sont visibles en pratique que pour z< 0.7.
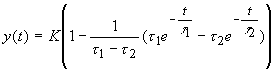 où
où
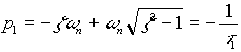 et
et
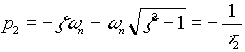
sont les pôles du systéme.
On remarque que y(0)=0 et
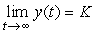 .
.
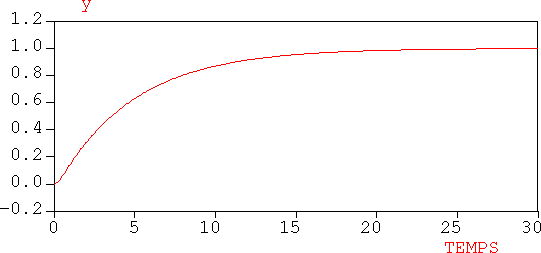
La courbe y(t) part donc de l'origine avec une tangente horizontale; elle tend vers l'asymptote y = K suivant un régime apériodique. y(t) est la combinaison linéaire d'une constante et de deux exponentielles décroissantes en fonction du temps, lorsque les deux constantes de temps sont positives.