Construction du diagramme de Bode à l'aide des asymptotes

On peut tracer approximativement le diagramme de Bode pour un système de n-ième ordre si on connaît la position des pôles et des zéros:

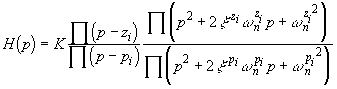
La valeur H(0) est le gain statique de système;

Pour chaque pôle simple réel negatif pi, le module de la réponse harmonique décroît de 20dB par décade à partir de la pulsation wi = pi et la phase de la réponse harmonique décroît de 90 °:

Pour le diagramme Bode-Gain l'erreur maximale entre le tracé exact et l'approximation asymptotique est 3dB et elle est atteinte pour la valeur de la pulsation .

Pour une paire de pôles complexes conjugués avec la partie réelle negative, le diagramme de Bode a l'allure suivante:

Pour chaque zéro réel, le module de la réponse harmonique a une croissance de 20dB par décade à partir de la pulsation wi =|zi| et la phase de H(j) a une croissance ou une décroissance de 90 ° en fonction du signe du zéro.

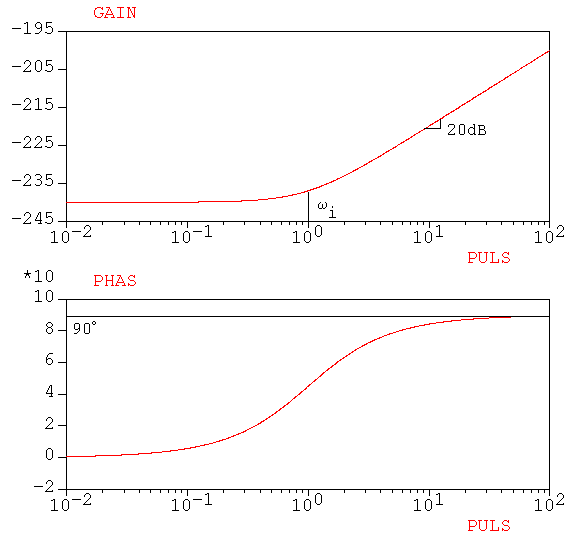
Pour le diagramme de Bode-Gain l'erreur maximale entre le tracé exact et l'approximation asymptotique est de 3dB et elle est atteinte pour la valeur .

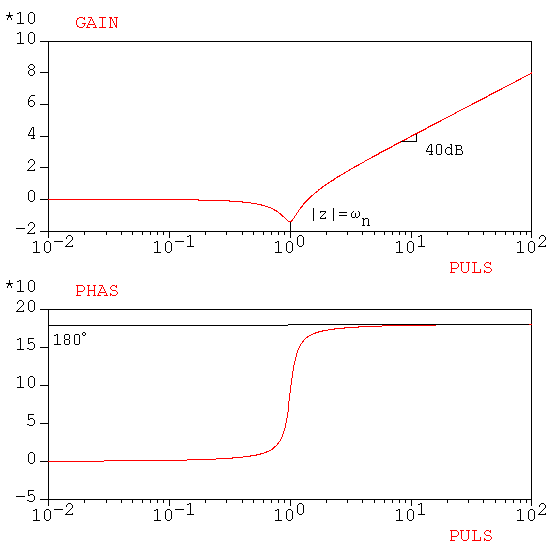
Dans le diagramme Bode-Gain une paire de zéros complexes conjugués est caractérisée par l'existence d'une rupture de pente: à partir de la pulsation le module de la réponse harmonique a une croissance de 40dB par décade.

Dans le diagramme Bode-Phase une paire de zéros complexes conjugués est caractérisé par une croissance ou décroissance de 180 ° en fonction de la partie réelle de zéros.