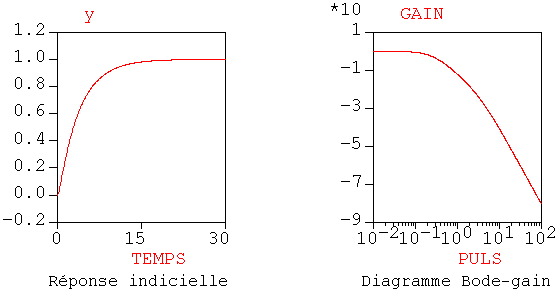
Lien entre le coefficient d'amortissement et les représentations temporelles et fréquentielles
Pour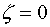 (cas théorique), on a un système sans amortissement, ou système juste oscillant;
(cas théorique), on a un système sans amortissement, ou système juste oscillant;
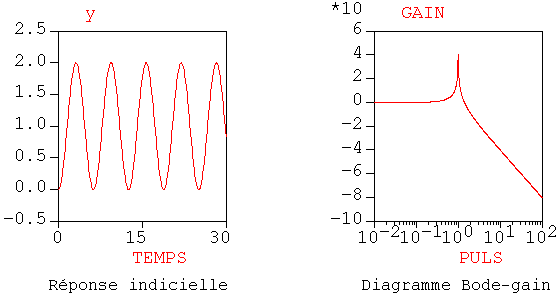
Pour
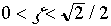 le système est amorti, résonant et oscillant;
le système est amorti, résonant et oscillant;

Plus z est faible, plus le système oscille longtemps et plus l'amplitude des oscillations est forte.
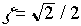
s'appelle amortissement critique et correspond à la valeur à partir de laquelle le système n'est plus résonant.
Pour
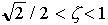 seules persistent les oscillations théoriques au niveau de la
réponse indicielle ou impulsionnelle, et qui deviennent de moins en
moins perceptibles quand z augmente. Le système est amorti, oscillant, non-résonant.
seules persistent les oscillations théoriques au niveau de la
réponse indicielle ou impulsionnelle, et qui deviennent de moins en
moins perceptibles quand z augmente. Le système est amorti, oscillant, non-résonant.
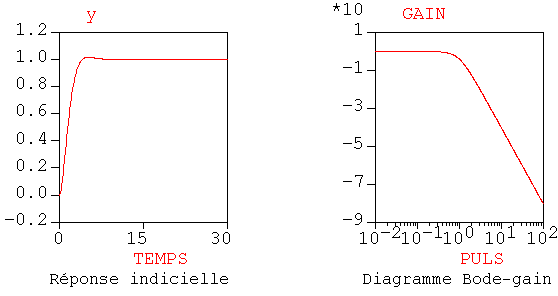
Pour
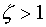 le système est amorti (hyper-amorti), non-résonant, non-oscillant
(apériodique);
le système est amorti (hyper-amorti), non-résonant, non-oscillant
(apériodique);