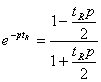Approximation d'un retard
Si le retard est très petit on peut l'approcher par :
![]()
On peut aussi l'approcher par une constante de temps.
Dans le cas où l'entrée est un échelon unitaire et où le retard tR est petit par rapport au temps de réponse du système, on peut en première approximation considérer le retard pur comme un système du premier ordre, de constante de temps tR.
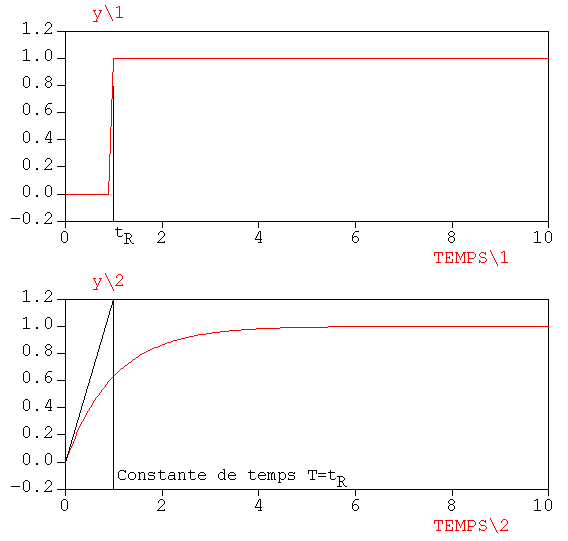
La ressemblance aux basses fréquences entre une constante de temps et un retard pur s'explique:
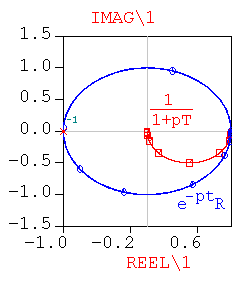
a) Graphiquement sur le diagramme de Nyquist parce que les courbes :
![]()
sont tangentes pour une pulsation nulle.
b) Analytiquement, sur les deux premiers termes du développement en série de
![]()
suivant les puissances croissantes de p, parce que ces termes sont les mêmes si T = tR, ce qui exprime l'égalité approximative.
On n'oubliera pas que ces ressemblances ne sont valables que lorsque tR est petit par rapport aux périodes des phénomènes qu'on étudie et ne sont pas valables aux moyennes et hautes fréquences
Enfin pour une étude plus précise on utilisera une approximation due à Pade :
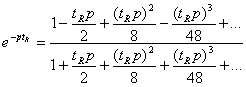
que l'on simplifie souvent au premier ordre :