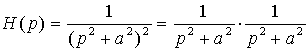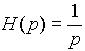La condition nécessaire et suffisante de stabilité (au sens de
Lyapunov) pour un système linéaire est la suivante:
tous les pôles de sa fonction de transfert doivent avoir leur partie réelle strictement négative.
C'est aussi ce qu'on appelle la stabilité asymptotique.

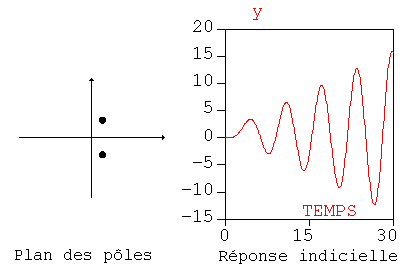
La réponse y(t) à une entrée u(t) pour un système linéaire ayant pour fonction de transfert
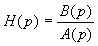
est donnée par
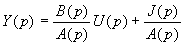
J(p) étant une fonction qui dépend des conditions initiales et
s'annule avec celles-ci.
Etudions le comportement du système lorsqu'il est abandonné à lui même. (u(t)=0)
La décomposition en éléments simples de la fraction rationnelle J(p)/A(p) donne:
a) des termes de la forme
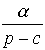 ,
correspondant aux racines réelles du polynôme A(p);
,
correspondant aux racines réelles du polynôme A(p);
b) des termes de la forme
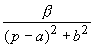 ,
correspondant aux racines complexes conjuguées de A(p) (de la
forme a+jb ou a-jb).
,
correspondant aux racines complexes conjuguées de A(p) (de la
forme a+jb ou a-jb).
C'est dire que la réponse y(t) est la somme de fonctions du temps de la forme:
Plusieurs cas sont alors à distinguer:
1. Les exponentielles ect et eat sont
toutes décroissantes, le système est dit asymptotiquement stable.
C'est le cas si tous les pôles de la fonction de transfert ont leur
partie réelle strictement négative.
2. Une au moins des exponentielles ect ou
eat est croissante, le système est dit instable. C'est
le cas si au moins une racine de A(p) a sa partie réelle
positive.
3. Le cas particulier où H(p) a une paire de pôles
imaginaires purs conjugués correspond à une réponse de
type sinusoïde non amortie: le système est dit juste oscillant, il
est à la limite de la stabilité.
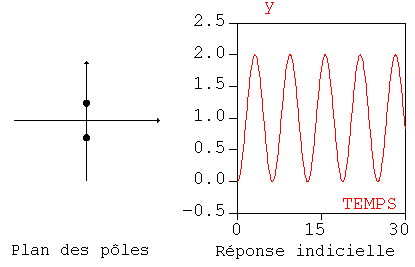
Si la paire de pôles imaginaires purs est d'ordre supérieur à un, le système est instable.
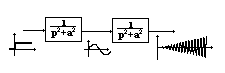
Par exemple dans le cas d'une paire double ce système est équivalent à deux
systèmes en cascade: le premier, juste oscillant répond à
une entrée en échelon par une sinusoïde de fréquence
égale à la fréquence de résonance du second système, qui joue à son tour le rôle d'entrée du
second bloc. D'où la divergence annoncée.
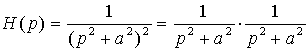
L'intégrateur pur de fonction de transfert :
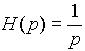
est un système stable mais non asymptotiquement stable (il ne vérifie pas la propriété
entrée bornée - sortie bornée).
[ Table des matières ]


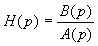
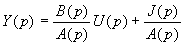
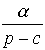 ,
correspondant aux racines réelles du polynôme A(p);
,
correspondant aux racines réelles du polynôme A(p);
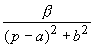 ,
correspondant aux racines complexes conjuguées de A(p) (de la
forme a+jb ou a-jb).
,
correspondant aux racines complexes conjuguées de A(p) (de la
forme a+jb ou a-jb).