Représentation d'état
Illustration
Considérons le circuit électrique ci-dessous:
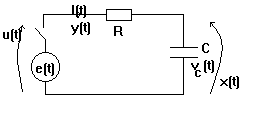
On peut énoncer le problème: fermons l'interrupteur au temps t=t0, cherchons l'évolution temporelle du courant I(t) dans le circuit considéré.
Utilisons la notation couramment admise:
- u(t) excitation, ici tension appliquée à l'entrée du circuit, e(t)
- x(t) état, ici tension aux bornes du condensateur, vc(t)
- y(t) sortie, ici courant circulant dans le circuit, I(t).
Le lecteur établira sans difficulté:
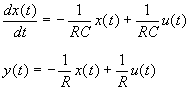
Soit u(t) une entrée échelon d'amplitude e0 et T=RC.
La valeur initiale x(t0) est imposée et définit l'état initial du circuit; les expressions de x(t) et y(t) s'écrivent:
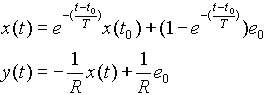
Représentons graphiquement ce résultat en choisissant trois valeurs différentes de x(t0): -1,0 et 1; prenons e0=1 volt.
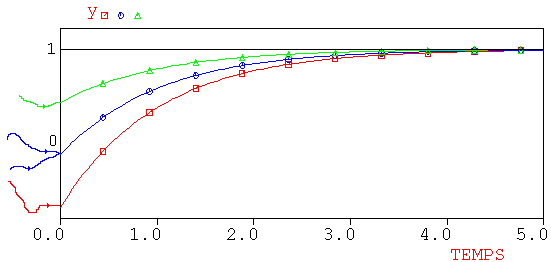
On remarque que:
- Pour déterminer x(t) et y(t) dans l'intervalle [t0 t], on n'a pas besoin de connaître ce qui s'est passé dans l'intervalle ]-¥ t0[, mais seulement l'état à l'instant t0, le chemin pris pour atteindre cet état n'important pas;
- à chaque état (x(t) dans notre exemple) correspond une valeur à t donné, ce qui permet de prévoir l'évolution du système. Si, au temps t1 >t0, on applique une nouvelle entrée u1(t), la sortie du système va évoluer, pour tÎ[t1 t] en fonction:
- du nouveau signal d'excitation, u1(t)
- de l'état du système en t1, soit x(t1).