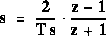Example: Digital DC Motor Speed Control with PID
Control
Continuous
to Discrete Conversion
PID
Controller
In this page, we will consider the digital control version of DC motor speed
problem. A digital DC motor model can be obtained from conversion of the analog
model, as we will describe. The controller for this example will be designed by
a PID method.
The open-loop transfer function for DC motor's speed was derived
as:
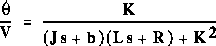
- Where:
- *electrical resistance (R) = 1 ohm
- *electrical inductance (L) = 0.5 H
- *electromotive force constant (Ke=Kt) = 0.01 Nm/Amp
- *moment of inertia of the rotor (J) = 0.01 kg*m^2/s^2
- *damping ratio of the mechanical system (b) = 0.1 Nms
- *input (V): Source Voltage
- *output (theta dot): Rotating speed
- *The rotor and shaft are assumed to be rigid
The design requirements for 1 rad/sec step input are
- Settling time: Less than 2 seconds
- Overshoot: Less than 5%
- Steady-state error: Less than 1%
Continuous to Discrete Conversion
The first step in designing a discrete
control system is to convert the continuous transfer function to a discrete
transfer function. Matlab command c2dm
will do this for you. The c2dm command requires the
following four arguments: the numerator polynomial (num), the denominator
polynomial (den), the sampling time (Ts) and the type of hold circuit. In this
example, the hold we will use is the zero-order
hold ('zoh').
From the design requirement, let the sampling time, Ts equal to 0.12
seconds, which is 1/10 the time constant of a system with a settling time of 2
seconds. Let's create a new m-file and
enter the following commands:
R=1;
L=0.5;
Kt=0.01;
J=0.01;
b=0.1;
num = Kt;
den = [(J*L) (J*R)+(L*b) (R*b)+(Kt^2)];
Ts = 0.12;
[numz,denz] = c2dm(num,den,Ts,'zoh')
Running this m-file should return the following:
numz =
0 0.0092 0.0057
denz =
1.0000 -1.0877 0.2369
From these matrices, the discrete transfer function can be
written as:
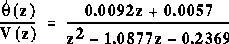
First, we would like to see what the closed-loop response of the system looks
like without any control. If you see the numz matrices shown above, it
has one extra zero in the front, we have to get rid of it before closing the
loop with the Matlab cloop command. Add the following
code into the end of your m-file:
numz = [numz(2) numz(3)];
[numz_cl,denz_cl] = cloop(numz,denz);
After you have done this, let's see how the closed-loop step response
looks like. The dstep command will generate the vector of
discrete output signals and stairs command will connect
these signals. Add the following Matlab code at the end of previous m-file and
rerun it.
[x1] = dstep(numz_cl,denz_cl,101);
t=0:0.12:12;
stairs(t,x1)
xlabel('Time (seconds)')
ylabel('Velocity (rad/s)')
title('Stairstep Response:Original')
You should see the following plot:

PID Controller
Recall that the continuous-time transfer function for a
PID controller is:
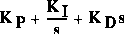
There are several ways for mapping from the s-plane to z-plane. The most
accurate one is 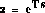 .
We cannot obtain PID transfer function in this way because the discrete-time
transfer function would have more zeroes than poles, which is not realizable.
Instead we are going to use the bilinear transformation shown as follows:
.
We cannot obtain PID transfer function in this way because the discrete-time
transfer function would have more zeroes than poles, which is not realizable.
Instead we are going to use the bilinear transformation shown as follows:
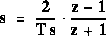
Thus we can derive the discrete PID controller with bilinear transformation
mapping. For more detail derivation of discrete PID controller. Equivalently, the c2dm command in
Matlab will help you to convert the continuous-time PID compensator to
discrete-time PID compensator by using the "tustin" method in this case. The
"tustin" method will use bilinear approximation to convert to discrete time of
the derivative. Kp = 100,
Ki = 200 and Kd = 10 are satisfied the
design requirement. We will use all of these gains in this example. Now add the
following Matlab commands to your previous m-file and rerun it in Matlab window.
% Discrete PID controller with bilinear approximation
Kp = 100;
Ki = 200;
Kd = 10;
[dencz,numcz]=c2dm([1 0],[Kd Kp Ki],Ts,'tustin');
Note that the numerator and denominator in c2dm were reversed above. The reason is that the PID transfer
function is not proper. Matlab will not allow this. By switching the numerator
and denominator the c2dm command can be fooled into
giving the right answer. Let's see if the performance of the closed-loop
response with the PID compensator satisfies the design requirements. Now add the
following code to the end of your m-file and rerun it. You should get the
following close-loop stairstep response.
numaz = conv(numz,numcz);
denaz = conv(denz,dencz);
[numaz_cl,denaz_cl] = cloop(numaz,denaz);
[x2] = dstep(numaz_cl,denaz_cl,101);
t=0:0.12:12;
stairs(t,x2)
xlabel('Time (seconds)')
ylabel('Velocity (rad/s)')
title('Stairstep Response:with PID controller')
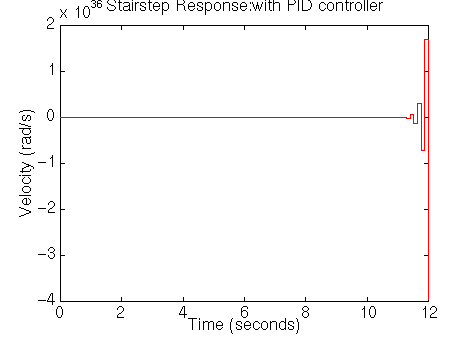
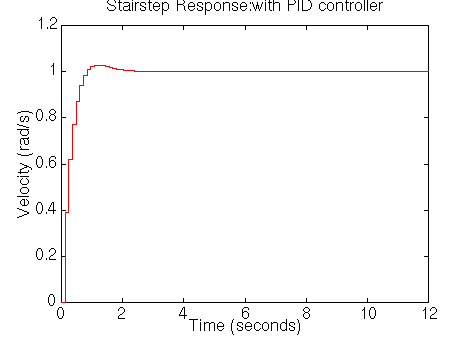
As you can see from the above plot, the closed-loop response of the system is
unstable. Therefore there must be something wrong with compensated system. So we
should take a look at root locus of the compensated system. Let's add the
following Matlab command into the end of your m-file and rerun it.
rlocus(numaz,denaz)
title('Root Locus of Compensated System')
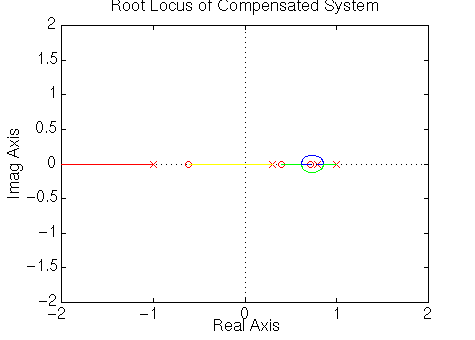
From this root-locus plot, we see that the denominator of the PID controller
has a pole at -1 in the z-plane. We know that if a pole of a system is outside
the unit circle, the system will be unstable. This compensated system will
always be unstable for any positive gain because there are an even number of
poles and zeroes to the right of the pole at -1. Therefore that pole will always
move to the left and outside the unit circle. The pole at -1 comes from the
compensator, and we can change its location by changing the compensator design.
We choose it to cancel the zero at -0.62. This will make the system stable for
at least some gains. Furthermore we can choose an appropriate gain from the root
locus plot to satisfy the design requirements using rlocfind.Enter the following Matlab code to your m-file.
dencz = conv([1 -1],[1.6 1])
numaz = conv(numz,numcz);
denaz = conv(denz,dencz);
rlocus(numaz,denaz)
title('Root Locus of Compensated System');
[K,poles] = rlocfind(numaz,denaz)
[numaz_cl,denaz_cl] = cloop(K*numaz,denaz);
[x3] = dstep(numaz_cl,denaz_cl,101);
t=0:0.12:12;
stairs(t,x3)
xlabel('Time (seconds)')
ylabel('Velocity (rad/s)')
title('Stairstep Response:with PID controller')
The new dencz will have a pole at -0.625 instead of -1, which almost
cancels the zero of uncompensated system. In the Matlab window, you should see
the command asking you to select the point on the root-locus plot. You should
click on the plot as the following:
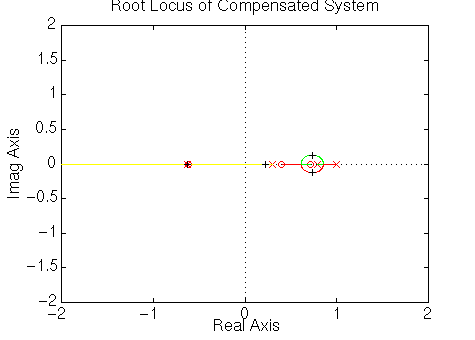
Then Matlab will return the appropriate gain and the corresponding
compensated poles, and it will plot the closed-loop compensated response as
follows.
The plot shows that the settling time is less than 2 seconds and the percent
overshoot is around 3%. In addition, the steady state error is zero. Also, the
gain, K, from root locus is 0.2425 which is reasonable. Therefore this response
satisfies all of the design requirements.
[ Table des matières ]
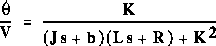
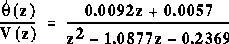

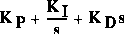
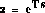 .
We cannot obtain PID transfer function in this way because the discrete-time
transfer function would have more zeroes than poles, which is not realizable.
Instead we are going to use the bilinear transformation shown as follows:
.
We cannot obtain PID transfer function in this way because the discrete-time
transfer function would have more zeroes than poles, which is not realizable.
Instead we are going to use the bilinear transformation shown as follows: