Proportional
control
PID
control
Tuning
the gains
From the main problem, the dynamic equations in transfer function form
are the following:
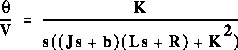
and the system schematic looks like:
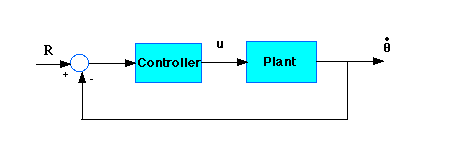
With a 1 rad/sec step reference, the design criteria are:
Proportional
control
PID
control
Tuning
the gains
From the main problem, the dynamic equations in transfer function form
are the following:
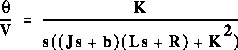
and the system schematic looks like:

With a 1 rad/sec step reference, the design criteria are:
Now let's design a PID controller and add it into the system. First create a new m-file and type in the following commands(refer to main problem for the details of getting those commands).
J=3.2284E-6; b=3.5077E-6; K=0.0274; R=4; L=2.75E-6; num=K; den=[(J*L) ((J*R)+(L*b)) ((b*R)+K^2) 0];Recall that the transfer function for a PID controller is:
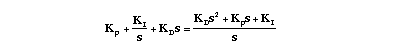
Let's first try using a proportional controller with a gain of 1.7. Add the following code to the end of your m-file:
Kp=1.7; numcf=[Kp]; dencf=[1]; numf=conv(numcf,num); denf=conv(dencf,den);To determine the closed-loop transfer function, we use the cloop command. Add the following line to your m-file:
[numc,denc]=cloop(numf,denf);Note that numc and denc are the numerator and the denominator of the overall closed-loop transfer function.
Now let's see how the step response looks. Add the following to the end of your m-file, and run it in the command window:
t=0:0.001:0.2; step(numc,denc,t)You should get the following plot:

Now lets take a look at the step disturbance response. Add the following to the end of your m-file, and run it in the command window:
numdcl=conv(numc,1); dendcl=conv(denc,Kp); step(numdcl,dendcl,t);You should get the following plot:
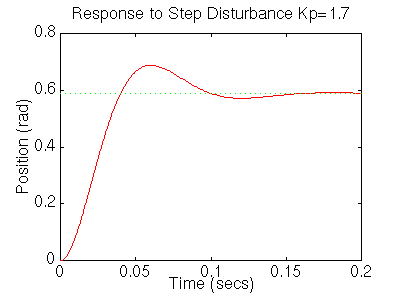
From the plots above we see that although the steady-state error looks good the settling time is too large, as is the overshoot. We also see that the steady-state error to a disturbance is large. Add an integral term will eliminate the steady-state error and a derivative term will reduce the overshoot. Let's first try a PI controller to get rid of the disturbance steady state error. Change your m-file so it looks like:
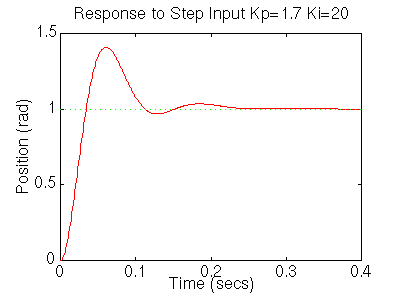
Lets see what happened to the step disturbance response, add the following to your m-file:
figure numdcl=conv(numc,dencf); dendcl=conv(denc,numcf); step(numdcl,dendcl,t);You should get the following plot:
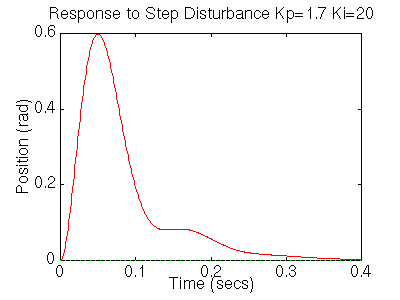
The settling time is still too long. Let's increase the gains in order to speed up the response. Go back to your m-file and change Ki to 200 and Kp to 17. Rerun the file and you should get plots like these:
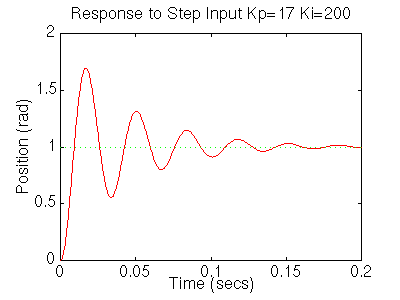
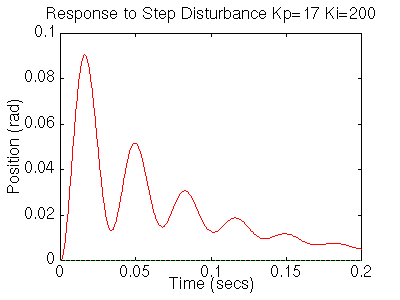
Now we see that the response is faster than before, but the large Ki has worsened the transient response (big overshoot). Let's now try a PID controller to reduce the overshoot. Go back to the m-file and make the following changes to look at the step response.
Kp=17; Ki=200; Kd=0.15; numcf=[Kd Kp Ki]; dencf=[1 0]; numf=conv(numcf,num); denf=conv(dencf,den); [numc,denc]=cloop(numf,denf,-1); t=0:0.001:0.1; step(numc,denc,t)Rerun it and you should get this plot:
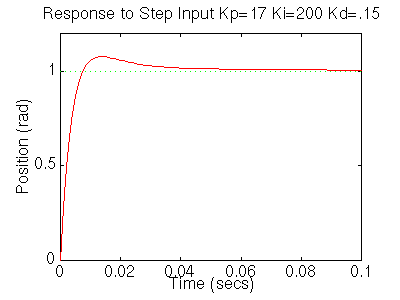
Your step disturbance plot should look like this:
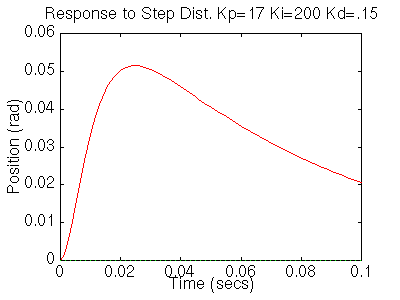
We now see that our step response looks really good, it has less than 16% overshoot and the settling time is roughly 40ms, and there is no steady-state error. However the step disturbance response is now really slow. Lets increase Ki to speed up the disturbance response. Change Ki to 600 in your m-file and rerun the file. You should get the following plots:
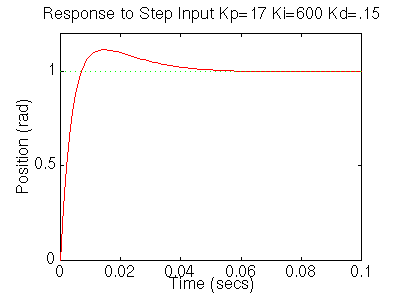
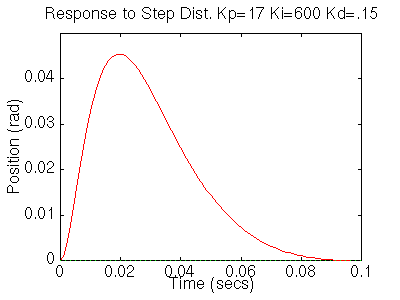
We now can see that the step response has a settling time of roughly 40ms, it has less than 16% overshoot, and it has no steady state error. The step disturbance response also has no steady state error. So now we know that if we use a PID controller with
Kp=17,
Ki=600,
Kd=.15,
all of our design requirements will be satisfied.