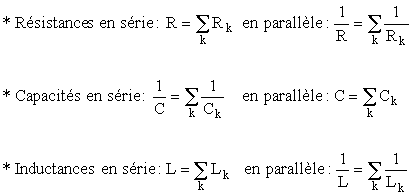
Le but de cette leçon est de présenter
quelques rudiments sur les signaux périodiques et de donner à
comprendre la notion d'impédance en électrotechnique.
Il est présenté des notations et des propriétés de signaux électriques. On s'intéresse dans ce cours à des signaux de nature déterministe, reportant à une introduction au traitement de signal la question des signaux de nature aléatoire. On rappelle les grandeurs définies et mesurables sur un signal périodique : sa fréquence, son amplitude, sa valeur efficace, sa valeur moyenne.
On définit aussi le concept de puissance instantanée et celui, plus utilisé, de puissance moyenne. La connaissance de la puissance fournie ou consommée par un dipôle est importante, tant sur le plan du bilan énergétique qui peut servir à vérifier des calculs que sur le plan strictement physique où l'énergie thermique crée dans un dipôle doit être évacuée d'une manière ou d'une autre vers l'extérieur.
Le régime sinusoïdal est d'une grande importance en électricité, comme en technique en général (voir la leçon consacrée à l'analyse fréquentielle). On définit les outils et grandeurs classiques: valeurs efficace et moyenne, amplitude, fréquence, puissances active et réactive, notation de Fresnel, impédance d'un dipôle, gain et atténuation en décibel.
On montre aussi le problème de l'association de dipôles, qui est de trouver des dipôles équivalents à des ensembles de dipôles montés en série ou en parallèle. Du moment que les caractéristiques des dipôles se résument à leur relation tension-courant, les lois de Kirchhoff expriment que les courants se somment en parallèle et que les tensions se somment en série. Si la caractéristique d'un dipôle est statique et non-linéaire, on peut appliquer facilement ces règles pour construire la caractéristique statique du dipôle équivalent. Le cas linéaire et dynamique des impédances est celui qui revient très fréquemment : les impédances se somment en série, et l'inverse de l'impédance équivalente est la somme des inverses des impédances montées en parallèle.
______________________________________________________
Table des matières
| 1. Caractéristiques
de signaux périodiques 1.1. Amplitude du signal 1.2. Fréquence du signal 1.3. Valeur crête-à-crête (peak-to-peak : ptp) 1.4. Valeur moyenne (average, mean) 1.5. Valeur efficace (root mean square : RMS ) |
2.
Puissance d'un dipôle 2.1. Puissance instantanée 2.2. Exemple et convention de signe 2.3. Puissance moyenne |
| 3. Régime
sinusoïdal 3.1. Grandeurs typiques en régime sinusoïdal 3.2. Puissances actives et réactives 3.3. Notation de Fresnel 3.4. Exemple : circuit RC en régime sinusoïdal 3.5. La notion d'impédance 3.6. Gain, atténuation et décibels |
4.
Associations d'impédances 4.1. Cas général d'association de dipôles 4.2. Association de dipôles non linéaires (caractéristique statique) 4.3. Association de dipôles linéaires |
_________________________________________________________________
____________________________________
______________________________________________________
1. CARACTERISTIQUES DE SIGNAUX PERIODIQUES
_____________
1.1. Amplitude du
signal
1.2. Fréquence du signal
1.3. Valeur crête-à-crête (peak-to-peak
: ptp)
1.4. Valeur moyenne (average, mean)
1.5. Valeur efficace (root mean square : RMS )
Soit un signal périodique.

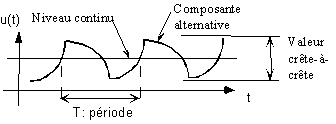
On définit les grandeurs suivantes: l'amplitude, la fréquence, la valeur crête-à-crête, la valeur moyenne, la valeur efficace.
Elle peut être définie crête à crête ou bien en valeur absolue
1.2.
Fréquence du signal
La fréquence est l'inverse
de la période :

1.3. Valeur crête-à-crête (peak-to-peak : ptp)
Selon dessin
1.4. Valeur moyenne (average, mean)
La valeur moyenne est donnée par :
![]()
Cette valeur moyenne est aussi appelée "niveau continu" ou "niveau DC" en électronique ; l'autre composante du signal est qualifiée d'alternative.
1.5. Valeur efficace (root mean square : RMS )
La valeur efficace est donnée par :
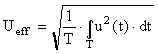
Cette valeur efficace correspond au niveau d'un signal continu qui produirait la même dissipation par effet Joule. Par exemple, si on devait calculer la dissipation thermique d'un élément sous l'effet d'un signal, la valeur efficace de ce dernier serait la valeur la plus utile.
______________________________________________________
2. PUISSANCE D'UN DIPOLE
_____________
2.1. Puissance instantanée
2.2. Exemple et convention de signe
2.3. Puissance moyenne
Nous avons vu précédemment l'analogie électromécanique, faisant correspondre tension à force et courant à vitesse. L'analogie peut donc se poursuivre dans l'expression de la puissance instantanée :

Remarquons que cette puissance électrique est la puissance mécanique à développer pour déplacer une charge dans un champ électrostatique, à une vitesse donnée.
2.2. Exemple et convention de signe
Une source débite dans un récepteur ohmique ; la puissance fournie par la source est négative. Pour le récepteur ohmique dont on a vu que sa caractéristique est de consommer de la puissance, le signe correspondant de la puissance est positif.
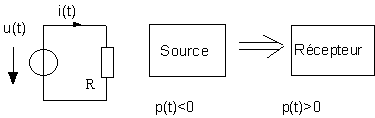
On a pour la source :
![]()
et pour la charge :
![]()
Un élément résistif dissipe toujours de la puissance : c'est sa caractéristique. Alors on a toujours une expression positive de la puissance. Mais pour des éléments non-consommateurs comme l'inductance par exemple, la puissance est parfois positive (l'inductance se charge en courant, donc soutire de l'énergie au circuit), parfois négative (l'inductance restitue de l'énergie au circuit électrique).
Ce qui exprime la consommation ou non de puissance n'est donc pas sa valeur instantanée, mais sa valeur moyenne.
L'expression de la puissance moyenne est donnée en toute généralité par :
![]()
______________________________________________________
3. REGIME SINUSOIDAL
_____________
3.1. Grandeurs typiques
en régime sinusoïdal
3.2. Puissances actives et réactives
3.3. Notation de Fresnel
3.4. Exemple : circuit RC en régime sinusoïdal
3.5. La notion d'impédance
3.6. Gain, atténuation et décibels
Une des caractéristiques des systèmes linéaires est de conserver la forme des signaux sinusoïdaux. Pour un tel système, on peut donc parler de régime sinusoïdal.
3.1. Grandeurs typiques en régime sinusoïdal
Pour un signal sinusoïdal exprimé, par :
![]()
on a :
| amplitude | |
| fréquence | |
| crête à crête | |
| valeur moyenne | |
| valeur efficace | 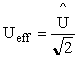 |
3.2. Puissances actives et réactives
Dans le cas où un récepteur consomme une puissance (moyenne), on parle de puissance active, c'est le cas de la résistance. L'énergie entre dans le système sous forme électrique, et en sort sous forme de pertes ohmiques. Notons que si le schéma électrique représente aussi en partie un système mécanique, la perte ohmique peut signifier des frottements visqueux, comme indiqué précédemment.
Dans le cas où l'on a une puissance moyenne nulle mais une puissance instantanée non nulle, on dit que la puissance est réactive, c'est le cas des inductances et capacités, des bobines et condensateurs de bonne qualité. L'énergie circule dans le circuit et se fait momentanément stocker (sous forme magnétique respectivement électrique pour l'inductance et la capacité). Le récepteur ne consomme pas à proprement parler de l'énergie, mais cette fluctuation de courant crée des pertes dans les lignes de transmission.
En régime sinusoïdal, les courants et tensions sont des sinusoïdes déphasées l'une par rapport à l'autre, et ayant chacune leur amplitude.
On représente les courants et tensions d'un dipôle par des vecteurs dits de Fresnel, où l'information de fréquence est laissée de côté.
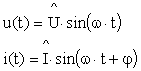
Vecteurs de Fresnel :
On ne garde dans cette représentation que la valeur efficace, image de l'amplitude et de déphasage entre courant et tension.
Ainsi, la puissance active devient le produit scalaire des deux vecteurs :

Le déphasage entre courant et tension d'un quart de tour correspond en régime sinusoïdal, à la relation de dérivation ou d'intégration existant entre ces grandeurs pour la capacité et l'inductance. Remarquons encore que dans cette notation, l'application des lois de Kirchhoff revient à fermer les polygones des tensions et courants.
3.4. Exemple : circuit RC en régime sinusoïdal
Circuit RC en régime sinusoïdal :
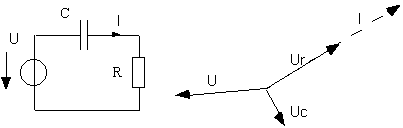
On constate que courant et tension sont parallèles dans la résistance, et perpendiculaires dans la capacité. La notion d'impédance, qui est abordée plus loin, permet de faire des calculs qui peuvent être complémentaires d'une méthode graphique de ce type. La représentation de Fresnel permet de "visualiser" une partie du comportement d'un système linéaire en régime sinusoïdal (dit aussi régime harmonique)
3.5.1. Justification théorique
La représentation vectorielle des relations courant-tension en régime sinusoïdal est une manière de ne garder du signal qu'un déphasage et une amplitude. Ce résultat peut aussi être obtenu grâce à l'utilisation de nombres complexes:
Le signal :
![]()
devient, en notation complexe :

La notation complexe permet d'exprimer la relation courant-tension en régime sinusoïdal, grâce à la notion d'impédance :

Cette relation prend la même forme linéaire que la loi d'ohm. L'utilisation de ces nombres complexes en régime sinusoïdal permet de traiter dans le même langage les effets résistifs, capacitifs et inductifs. (Voir l'exercice 5.6).
3.5.2. Impédance des trois éléments passifs de base
| Caractéristique | Relation i-u: | Impédance | |
| Résistance | |||
| Inductance | |||
| Capacité |
3.5.3. Impédance d'une bobine
On peut modéliser le comportement linéaire d'une bobine auto inductive de la sorte :
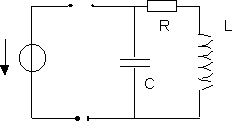
La résistance représente les pertes par effet Joule, l'inductance la composante auto inductive, la capacité les effets d'accumulation de charges.
3.5.4.
Impédance d'un condensateur
On modélise souvent un condensateur en tenant compte de ses pertes ohmiques :
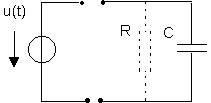
Ces pertes sont représentées, en mode fréquentiel, par un angle de pertes d'autant plus petit qu'elles sont faibles :
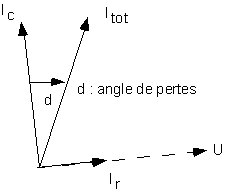
3.6. Gain, atténuation et décibels
Il arrive fréquemment, notamment lors d'analyses harmoniques (voir la leçon consacrée à l'analyse fréquentielle), que l'on veuille exprimer le gain d'un système en décibels. Que cela signifie-t-il ?
3.6.1. Gain
Le gain en général est défini comme le rapport de la grandeur de sortie sur celle d'entrée:
 |
3.6.2. Gain en puissance
Le gain en puissance d'un système peut être exprimé en logarithme et l'unité est alors le Bel ou le décibel :
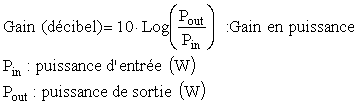
Comme en électronique on travaille souvent directement en tension ou courant, il faut encore voir qu'une puissance électrique est donnée par le carré de ces grandeurs. Il en résulte :

3.6.3. Exemple d'un filtre passe-bande
Un filtre électronique présente la propriété d'avoir un gain en tension variable en fréquence :
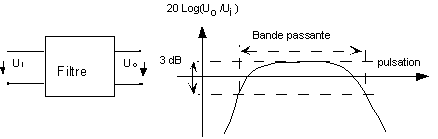
La région en fréquence délimitée par une chute de gain inférieure à 3 dB est appelée bande passante.
______________________________________________________
4. ASSOCIATIONS D'IMPEDANCES
_____________
4.1. Cas général
d'association de dipôles
4.2. Association de dipôles non linéaires
(caractéristique statique)
4.3. Association de dipôles linéaires
4.1. Cas général d'association de dipôles
Des deux relations de Kirchhoff, on déduit immédiatement les règles d'association des dipôles :
4.1.1. Association en parallèle
|
|
|
4.1.2. Association en série
|
|
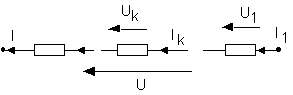
|
4.2. Association de dipôles non linéaires (caractéristique statique)
Soit une diode mise en parallèle à une résistance. Le dipôle résultant est également non-linéaire, et on peut aisément reconstituer sa caractéristique statique en sommant les courants.
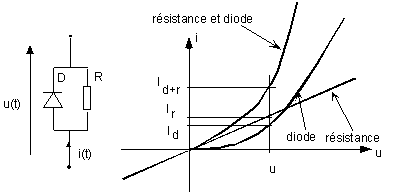
4.3. Association de dipôles linéaires
4.3.1. Impédances pour les dipôles linéaires
Dans le cas plus standard des dipôles linéaires, on a pour leurs impédances :
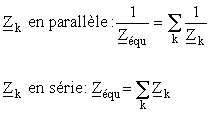
4.3.2. Cas des trois dipôles passifs de base :