Le but de cette leçon est d'aborder les trois composants passifs linéaires de base en électrotechnique avec leurs notation, caractéristique courant-tension et effets physiques correspondants.

Les trois effets fondamentaux en électrotechnique sont présentés: les effets résistif, capacitif et auto inductif. Ils sont mis en relations avec leur formulation mathématique et leurs éléments électrotechniques.

On aborde aussi l'analogie avec les équations de la mécanique où l'on voit que la résistance correspond à la formulation électrotechnique de la dissipation thermique d'énergie, la capacité le stockage d'énergie potentielle et l'inductance le stockage d'énergie sous forme cinétique, la loi des mailles correspondant à une des lois de Newton.

Table des matières

1.1. Effet résistif
1.2. Loi d'ohm
1.3. La résistance : phénomène physique
1.4. La résistance : concept électrotechnique
1.5. La résistance : des composants technologiques
1.6. Résistance d'une tige conductrice
1.7. Linéarité et autonomie d'une résistance
1.8. Analogie mécanique de la résistance

1.1. Effet résistif

Il convient de noter que la dégradation d'énergie en forme thermique est un phénomène général en physique, phénomène décrit par la thermodynamique. En électricité, si on place une tension aux bornes d'un conducteur, il advient un courant. La dissipation d'énergie se manifeste par un échauffement et une chute de potentiel le long du conducteur ; il y a conversion d'énergie électrostatique (contenue dans le générateur par exemple) en énergie thermique (échauffement par effet Joules).

 1.2. Loi d'ohm

Lorsqu'on branche un conducteur à une tension donnée, il résulte un courant, dont l'intensité dépend de la résistance du conducteur à son passage.

La loi d'Ohm exprime que certains matériaux ont un comportement linéaire :

En termes des circuits et systèmes :

 1.3. La résistance : phénomène physique

Le phénomène physique de résistivité correspond à la résistance qu'offre l'élément au passage du courant. On écrit :

C'est une expression de la dissipation thermique (effet Joule) ; du point de vue du circuit, la résistance ne stocke pas d'énergie, mais la dissipe. La puissance instantanée vaut :

 1.4. La résistance : concept électrotechnique

Le concept de résistance est défini comme le rapport de la tension sur le courant :

1.4.1. Résistance statique :

1.4.2. Résistance dynamique :


La résistance dynamique est définie comme le rapport des accroissements de courant sur ceux de tension, à un point de fonctionnement donné

.

Par exemple, dans le cas de la caractéristique courant-tension d'un dipôle non linéaire comme la diode, on définit sa résistance dynamique ainsi :

1.4.3. symbole associé :

1.5. La résistance : des composants technologiques

Sous le même terme de "résistance", on désigne encore le composant, mis en oeuvre technologiquement.

Il s'agit ici de l'élément le plus simple, très utilisé en électronique.

Il existe des séries de résistances normalisées. La série E12 est la plus courante. Voir les valeurs en laboratoire.

Extrait de fiche technique d'une résistance :

Symbole associé :

Cet élément peut servir de résistance variable manuellement, si l'on connecte deux des trois bornes ensemble.

Le symbole est aussi parfois utilisé pour exprimer que dans un circuit, la valeur de la résistance est commandée.

Extrait de fiche technique d'un potentiomètre :

- Les Photorésistances dont la valeur de la résistance dépend de l'éclairement et constituées d'inclusions de sulfure de cadmium dans du plastique.

- Les Thermistances dont la valeur de la résistance dépend de la température.

- Les Varistances (en anglais voltage dependent resistor), dont la valeur de la résistance est fonction de la tension appliquée.

1.6. Résistance d'une tige conductrice

1.7. Linéarité et autonomie d'une résistance

Remarquons encore qu'une résistance n'est pas forcément linéaire ni forcement autonome (indépendante du temps) : lorsqu'on modélise un capteur ou un effet physique, à peu près tout peut arriver ! Il existe par exemple des résistances dont la valeur varie fortement avec la température ambiante (thermistances) ; elles peuvent être utilisées comme détecteurs ou capteurs de température.

Pour un conducteur normal, on peut utiliser une approximation linéaire en la température, si le modèle autonome est insuffisant :

1.8. Analogie mécanique de la résistance

En mécanique, le travail de forces de frottement représente une dissipation d'énergie du système considéré. Une de leur modélisation correspond aux forces dites de frottement visqueux, où leur intensité est proportionnelle à la vitesse de déplacement. Si on écrit la loi d'Ohm en terme de charge et de tension, on observe une similitude :

Il est clair que ni la relation courant-tension dans une résistance n'est toujours aussi simple, ni les forces de frottement toujours visqueuses et linéaires. Il s'agit en fait d'une rationalisation technique : on construit des systèmes technologiques auxquels on impose cette simplicité dans des limites de fonctionnement. Par exemple, la valeur de la résistance dépend de la température de cette dernière : elle augmente avec la température. Alors on s'arrange pour écouler la chaleur et ainsi maintenir les systèmes dans leurs plages de fonctionnement.

2.1. Effet auto inductif
2.2. Coefficient d'auto-induction et caractéristique d'une inductance
2.3. L'auto-induction : un phénomène physique
2.4. L'inductance : un concept électrotechnique
2.5. La bobine : un composant technologique
2.6. Inductance d'un solénoïde
2.7. Linéarité, autonomie
2.8. Analogie mécanique de l'inductance

2.1. Effet auto inductif

Lorsqu'un courant circule dans un conducteur, il est responsable de la création d'un champs d'induction magnétique. Si le courant est variable dans le temps, le champs d'induction le sera aussi et alors intervient le phénomène d'auto-induction : ce champs variable rétroagit sur le courant qui le crée, en ralentissant la variation de ce courant. Cet effet correspond à un stockage d'énergie dans le circuit auto-inductif, sous forme magnétique.

2.2. Coefficient d'auto-induction et caractéristique d'une inductance

Un courant constitue une source de champ d'induction magnétique. Lorsqu'un courant circule dans un circuit , on conçoit que la surface sous-tendue par ce circuit subit un flux d'induction magnétique :

Pour un circuit donné, on définit son coefficient d'auto-induction, comme le rapport du flux sur le courant le générant, soit en fait sa capacité à emmagasiner du champ, de l'énergie magnétique :

En appliquant la loi d'induction, on obtient pour la caractéristique courant-tension :

et avec le coefficient L constant (c'est à dire : inductance autonome et linéaire), on obtient la relation standard:

La caractéristique d'une inductance est donc dynamique, puisqu'elle fait intervenir la dérivée temporelle du courant, contrairement à ce qu'il arrive avec une résistance standard, vue précédemment. En termes intuitifs, on peut dire que c'est un élément qui s'oppose aux fortes variations de courant, car pour obtenir des variations de courant, il faut des tensions proportionnelles à ces variations.

2.3. L'auto-induction : un phénomène physique

Le phénomène physique correspond au stockage d'énergie sous forme magnétique. Le stockage est momentané et l'énergie est restituée au circuit en courant.

L'énergie accumulée par l'élément auto inductif vaut :

2.4. L'inductance : un concept électrotechnique

Le concept d'auto-inductance, qui peut être défini comme précédemment.

Symbole associé :

2.5. La bobine : un composant technologique

La bobine est l'élément technologique correspondant.

Extrait de fiche technique d'une bobine miniatur:e

Extrait de fiche technique d'une bobine d'accumulation :

2.6. Inductance d'un solénoïde

On a pour un solénoïde :

2.7. Linéarité, autonomie

La caractéristique d'une bobine peut facilement devenir non-linéaire, à cause de la saturation du champ d'induction, ainsi que de phénomènes d'hystérèses :

Un exemple d'inductance non-autonome est fourni par un capteur de position : une ferrite se déplace dans un bobinage et l'inductance varie en conséquence. Dans ce cas, le but de l'électronique en aval est de produire une information de position :

2.8. Analogie mécanique de l'inductance

En mécanique, le bilan des forces extérieures agissant sur un système est responsable d'une accélération de ce système (Newton). Il s'agit donc de variation de l'énergie cinétique du système. On écrit, comme précédemment, la caractéristique de l'inductance en terme de charges et tension, d'où on observe à nouveau une similitude :

Comme dans le cas de la résistance, la même remarque peut être faite concernant la rationalisation technique que représentent les relations de l'inductance. La saturation des inductances bobinées (bobines) est une limitation tout à fait pratique de la linéarité de ces éléments.

3.1. Effet capacitif
3.2. Capacité et caractéristique courant-tension
3.3. L'accumulation de charges : un phénomène physique
3.4. La capacité : un concept électrotechnique
3.5. Le condensateur : un élément technologique
3.6. Capacité d'un condensateur à plaques
3.7. Linéarité et autonomie des condensateurs
3.8. Analogie mécanique de la capacité

3.1. Effet capacitif

Cet effet correspond au troisième phénomène très important. Lorsqu'on applique une différence de potentiel à deux conducteurs isolés les uns des autres, on assiste à une accumulation de charges par influence électrostatique. C'est cela l'effet capacitif. Il peut être ardemment recherché et dans ce cas on fabrique des condensateurs précis ou de grande capacité. Très souvent, l'effet capacitif est présent à titre parasitaire comme par exemple lors d'accumulation de charges entre deux lignes conductrices. Dans ce cas, on cherche à minimiser ses effets sur le temps de réponse de la ligne.

3.2. Capacité et caractéristique courant-tension

Pour un circuit donné, on définit sa capacité C comme le rapport de la charge accumulée sur la tension appliquée à ses bornes, soit en fait son aptitude à emmagasiner des charges électriques, de l'énergie électrostatique :

En dérivant cette dernière relation on obtient, pour la caractéristique courant-tension :

et avec la capacité C constante, c'est-à-dire autonome et linéaire, on obtient :

Comme la caractéristique de l'inductance, celle de la capacité est dynamique. En termes intuitifs, on peut dire que c'est un élément qui s'oppose aux fortes variations de tension, car il faut des courants proportionnels à ces variations.

3.3. L'accumulation de charges : un phénomène physique

Le phénomène physique correspond au stockage d'énergie sous forme électrostatique. Le stockage est momentané et cette énergie est restituée au circuit en tension.

L'énergie accumulée par l'élément capacitif vaut :

3.4. La capacité : un concept électrotechnique

Le concept de capacité est défini comme énoncé précédemment.

Symbole associé :

3.5. Le condensateur : un élément technologique

Le condensateur est l'élément technologique correspondant.

Extrait de fiche technique d'un condensateur électrolytique :

Extrait de fiche technique d'un condensateur au tantale :

- Les condensateurs à diélectrique film plastique (polypropylène, polystyrène, polyester...) le diélectrique a une permittivité relative de l'ordre de 2 à 3, les gammes de capacités s'étendent entre 100 pF et 10 µF.

Pour des applications où de fortes valeurs de capacités sont nécessaires, on a recours aux condensateurs au tantale (volume réduit), dans le domaine des hautes fréquences (1 MHz à 1 GHz) il faudra utiliser des condensateurs céramiques hyperfréquences.

- Les condensateurs électrochimiques aluminium sont constitués de deux armatures en aluminium séparées par un électrolyte gélifié en borate d'ammonium. Par électrolyse une fine couche d'alumine isolante se forme par oxydation sur l'anode et constitue le diélectrique.

Les valeurs des capacités sont élevées (jusqu'à 100 mF) mais ces condensateurs présentent l'inconvénient d'être polarisés (+ pour l'armature positive).

- Dans la même famille nous trouvons les condensateurs au tantale, peu coûteux, de dimensions plus réduites, sont polarisés également, mais travaillent généralement sous des tensions plus faibles que les condensateurs aluminium.

- Les condensateurs à papier paraffiné, dont les armatures sont constituées par des feuilles d'aluminium, le diélectrique étant le papier paraffiné, le tout enroulé. Leurs capacités peuvent atteindre quelques µF.

- Les condensateurs céramiques ont des armatures en aluminium séparées par un diélectrique au titanate de baryum ; les capacités vont du pF au µF.

- Les condensateurs au mica sont constitués par un empilement de feuilles de mica aluminisées sur les deux faces, formant une association de condensateurs en parallèles, les capacités peuvent atteindre quelques µF.

- Les condensateurs variables à lame d'air constitués de deux paires d'armatures, dont l'une mobile par rapport à l'autre sont utilisés pour "accorder" des circuits en fréquence.

3.6. Capacité d'un condensateur à plaques

On a pour un condensateur à plaque :

3.7. Linéarité et autonomie des condensateurs

Les problèmes de linéarité des condensateurs sont plutôt rares, mais pas exclus, puisqu'on peut aussi obtenir une saturation et une hystérèse du champ de déplacement électrique, comme vu précédemment pour le champ d'induction magnétique.

Un exemple de capacité non autonome est donné par des capteurs capacitifs : on peut contrôler l'épaisseur de fines couches d'isolants, s'ils sont suffisamment diélectriques, en mesurant la capacité de plaques entre lesquelles passent des feuilles d'isolant à tester.

3.8. Analogie mécanique de la capacité

En mécanique, une partie de l'énergie mécanique d'un système peut être emmagasinée dans des éléments dit élastiques, comme des lames. Il s'agit d'une énergie potentielle liée à des éléments dits ressorts, et on modélise la force de rappel linéairement en la position, pour les petites variations de cette dernière. De nouveau, on écrit la caractéristique de la capacité en termes de tension et charge, et on constate le même type d'analogie que précédemment pour l'inductance et la résistance :

4.1. L'analogie électromécanique : un outil d'interfaçage.
4.2. Le transformateur
4.3. Circuit RLC et oscillateur mécanique
4.4. Relation courant-tension : loi d'ohm généralisée

4.1. L'analogie électromécanique : un outil d'interfaçage.

Nous avons vu précédemment que la résistance, la capacité et l'inductance expriment, pour un système électrique, des concepts respectivement proches du frottement, accumulation d'énergie potentielle dans un ressort, accumulation d'énergie cinétique dans une masse, pour un système mécanique.

Il y a certes un intérêt théorique à la validité de cette analogie ; cette mécanique et cette électricité sont sous-tendues par la même approche de la physique classique. Sur un plan plus technologique, on peut dire que cette dimension sous-jacente étends le domaine d'application de l'outil de Kirchhoff à la mécanique. L'intérêt majeur de cette approche "circuits et systèmes" vient du fait qu'elle fonctionne non seulement pour des problèmes strictement électriques ou mécaniques, mais encore pour des problèmes d'ingénieurs où l'interfaçage entre les deux domaines doit être assuré. Nous évoquons ici le cas du transformateur électrique, dont le modèle peut servir à analyser certains moteurs électriques (actuateurs).

4.2. Le transformateur

Le transformateur électrique est un système à induction mutuelle. Il est constitué de deux enroulements électriques : l'un est le siège de la production d'un flux d'induction magnétique, l'autre est le siège de la captation de ce flux, ou du moins d'une partie de ce flux.

On représente un transformateur de la sorte :

De la loi d'induction, on sait que l'amplification est donnée par :

Extrait de fiche technique d'un transformateur pour circuit imprimé :

Utilisation dans un réseau électrique. Typiquement, on utilise un transformateur pour convertir des niveaux de tensions :

Une tension véhiculant une information peut être considérée selon deux modalités différentes :

* La tension est prise entre deux bornes et elle est dite différentielle. Par exemple si on veut mesurer un courant en plaçant dans une ligne une résistance, il faut prendre l'information de courant aux bornes de cette dernière.

* On crée une tension standard qu'on définit comme étant à potentiel nul, et on l'appelle la masse. Dans ce cas, l'information contenue dans un signal peut être lue sur une seule ligne. C'est généralement le cas. On peut parler de qualité de masse dans la mesure où cette dernière étant le siège de courants, elle est donc aussi le siège de chutes de tension. Elle n'est donc pas toujours stable ni précise, d'où la nécessité parfois de découpler les masses de deux circuits qui pourtant ont besoin de se communiquer des informations.

La tension d'entrée est référencée à la masse 1, alors que celle de sortie l'est à la masse 2. Il s'agit d'un découplage de masse, découplage dit galvanique.

La terre est une connexion à la terre physique, c'est à dire aux bâtiments, radiateurs, etc. ......

La terre est symbolisée de la sorte :

Le transformateur permet aussi de découpler (galvaniquement) les masses, grâce au couplage magnétique assurant la transmission de la puissance électrique. La masse du réseau est une masse de puissance, peu précise, subissant des parasites, alors que celle qu'on emploie en électronique doit être aussi propre, stable que possible, d'où un autre avantage du transformateur. Ce dernier est parfois même utilisé uniquement pour cette raison : deux circuits doivent se transmettre de l'information, mais les masses doivent rester découplées.

Plaçons le transformateur en situation, c'est à dire alimenté par une source affine et chargé par un dipôle réel. Pour la modélisation la plus simple, on obtient :

Avec:

La résistance R à l'entrée du quadripôle équivalent exprime le fait que le transformateur doit soutirer de la puissance à la source pour pouvoir en fournir à la charge.

Les puissances mises en jeu dépendent de la charge placée en bout du transformateur :

Par identification de R dans les expressions des puissances entrantes et sortantes, on obtient une valeur de la résistance d'entrée :

Notons encore que le transformateur, dans ce modèle, ne dissipe pas d'énergie. La résistance d'entrée n'est donc que l'image du transfert de puissance vers la partie droite du système.

On peut aussi tenir compte, dans la modélisation du transformateur, des résistances des bobinages, de leurs inductances parasites :

Ce modèle amélioré de transformateur peut servir de base à la théorie des moteurs alternatifs, en vertu de la possible modélisation électrique de phénomènes mécaniques. Dans ce cas, la résistance de sortie modélise des frottements mécaniques, l'inductance de sortie une charge d'inertie sur l'arbre moteur. On consultera au sujet des moteurs " : Transducteurs électromécaniques".

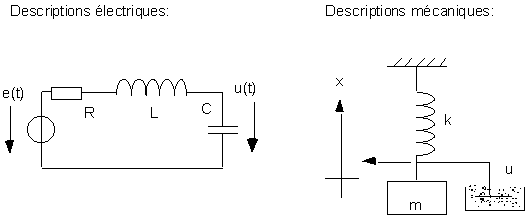
4.3. Circuit RLC et oscillateur mécanique

L'analogie électromécanique nous permet d'exprimer de deux manières différentes les oscillateurs harmoniques, à la base de nombreux modèles descriptifs en physique.

4.4. Relation courant-tension : loi d'Ohm généralisée

Nous avons vu que la loi d'Ohm, avec sa relation linéaire et statique courant-tension, permettait de modéliser la dissipation de puissance. Les deux relations courant-tension dynamiques de l'inductance et de la capacité peuvent-elles trouver une forme proche de cette loi d'Ohm, puisque des trois éléments sont "fondamentaux" ? Nous verrons à la leçon suivante qu'au travers de la notion d'impédance, valable en régime sinusoïdal, on peut unifier la notation et les règles de calculs, pour ces trois éléments.