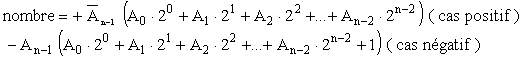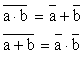______________________________________________________
SYSTÈMES LOGIQUES COMBINATOIRES
On y présente rapidement
les codes binaires, Gray et BCD, à titre d'introduction générale.
On rappelle les opérations et notations logiques de base, ainsi
que les instruments que sont les théorèmes, la table de vérité
et la table de Karnaugh.
______________________________________________________
Table des matières
1.
Quelques codes
1.1. Code binaire pur
1.2. Code en complément à deux
1.3. Code Gray
1.4. Code BCD |
2. Opérations
logiques booléennes de base
2.1. Opération ET (AND)
2.2. Opération OU (OR)
2.3. Opération NON (NOT)
2.4. Opération NON-ET (NAND)
2.5. Opération NON-OU (NOR)
2.6.Opération OU-EXCLUSIF (XOR) |
3. Logique Combinatoire
3.1. Définition
3.2. Table de Vérité
3.3. Table de Karnaugh
3.4. Théorèmes logiques |
____________________________________________________________________________________________________
______________________________________________________
1. QUELQUES
CODES
_____________
1.1. Code binaire
pur
1.2. Code en complément à deux
1.3. Code Gray
1.4. Code BCD
1.1.
Code binaire pur
* Le binaire pur est le codage en
base deux :
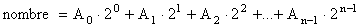
* Représentation graphique d'un mot binaire
:
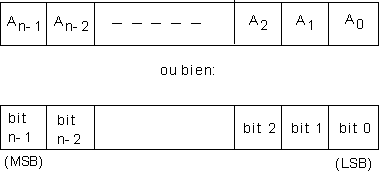
* Taille usuelle des mots binaires :
|
Taille du mot
|
Valeurs en binaire |
|
8 bits
|
0 - 255 |
|
16 bits
|
0 - 65535 (64 K) |
|
32 bits
|
0 - 4294967295 (4096 M) |
Note: En informatique, 1 K =1024.
* Notation hexadécimale :
Avec un mot de 4 bits, on peut compter de 0 à
15, ce que l'on peut noter : 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. La notation
hexadécimale correspond à l'utilisation de la base 16. Par
exemple : 50E6 (hex) = 20710 (déc)
* Exemple : comptage sur 4 bits :
|
Nombre décimal
|
Nombre binaire pur
|
Nombre hexadécimal
|
|
0
|
0 0 0 0
|
0
|
|
1
|
0 0 0 1
|
1
|
|
2
|
0 0 1 0
|
2
|
|
3
|
0 0 1 1
|
3
|
|
4
|
0 1 0 0
|
4
|
|
5
|
0 1 0 1
|
5
|
|
6
|
0 1 1 0
|
6
|
|
7
|
0 1 1 1
|
7
|
|
8
|
1 0 0 0
|
8
|
|
9
|
1 0 0 1
|
9
|
|
10
|
1 0 1 0
|
A
|
|
11
|
1 0 1 1
|
B
|
|
12
|
1 1 0 0
|
C
|
|
13
|
1 1 0 1
|
D
|
|
14
|
1 1 1 0
|
E
|
|
15
|
1 1 1 1
|
F
|
1.2. Code
en complément à deux
Ce code sert à représenter des nombres négatifs.
Pour cela on utilise le bit de poids fort pour le signe : "1"
pour les nombres négatifs et "0" pour les nombres positifs.
Le codage suivant permet d'additionner des nombres quelconques, dans les
limites de tailles des mots :
|
Nombre décimal
|
Codage en complément à deux
|
|
+3
|
0 1 1
|
|
+2
|
0 1 0
|
|
+1
|
0 0 1
|
|
0
|
0 0 0
|
|
-1
|
1 1 1
|
|
-2
|
1 1 0
|
|
-3
|
1 0 1
|
|
-4
|
1 0 0
|
On a pour le codage :
Exemple: Additionnons en complément
à deux : -3+2= ?
101
010
----
111 --> -1
1.3. Code
Gray
Il existe des systèmes, où l'on a avantage
à ce que d'une valeur à l'autre, il n'y ait qu'un seul bit
qui varie. Ce n'est pas le cas du binaire, où pour passer de 1 à
2 par exemple, deux bits changent. Si un capteur produit une information
codée, les transitions ne sont pas simultanées et on peut
lire : 1 (001) ->3 (011) ->2 (010) ou bien:
1 (001) ->0 (000) ->2 (010).
D'où le code Gray :
| Nombre décimal |
Codage Gray |
|
0
|
000
|
|
1
|
001
|
|
2
|
011
|
|
3
|
010
|
|
4
|
110
|
|
5
|
111
|
|
6
|
101
|
|
7
|
100
|
1.4. Code
BCD.
Le code binaire codé décimal (Binary Coded
Decimal) consiste à coder en binaire chaque digit du code décimal.
Par exemple, pour coder le nombre 529 :
529 = 5*100 + 2*10 + 9 (décimal) = 0101 1010 1001 (BCD)
Ce code est pratique pour afficher en décimal des nombres. Voir
l'exercice plus loin.
______________________________________________________
2. OPÉRATIONS
LOGIQUES
BOOLÉENNES DE
BASE
_____________
2.1. Opération ET(AND)
2.2. Opération OU(OR)
2.3. Opération NON (NOT)
2.4. Opération NON-ET (NAND)
2.5. Opération NON-OU (NOR)
2.6.Opération OU-EXCLUSIF (XOR)
2.1.
Opération ET (AND)
Symbole électronique :
|
Ecriture: 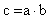
|
Fonction logique :
a b c
---------------
0 0 0
0 1 0
1 0 0
1 1 1
|
La porte ET détecte le cas où toutes
ses entrées sont à l'état haut (1).
2.2. Opération
OU (OR)
Symbole électronique :
|
Ecriture : 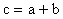
|
Fonction logique :
a b c
---------------
0 0 0
0 1 1
1 0 1
1 1 1
|
La porte OU détecte le cas où toutes
ses entrées sont à l'état bas (0).
2.3. Opération
NON (NOT)
Symbole électronique :
Ecriture: 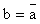
Fonction logique :
a b
-------
0 1
1 0
2.4. Opération
NON-ET (NAND)
Symbole électronique :
Ecriture: 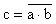
Fonction logique :
a b c
---------------
0 0 1
0 1 1
1 0 1
1 1 0
2.5. Opération
NON-OU (NOR)
Symbole électronique :
Ecriture 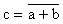
Fonction logique :
a b c
---------------
0 0 1
0 1 0
1 0 0
1 1 0
2.6.
Opération
OU EXCLUSIF (XOR)
Symbole électronique :
Ecriture: 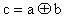
Fonction logique :
a b c
---------------
0 0 0
0 1 1
1 0 1
1 1 0
La porte OU EXCLUSIF détecte le cas où ses entrées
sont différentes.
______________________________________________________
3. LOGIQUE
COMBINATOIRE
_____________
3.1. Définition
3.2. Tabled de vérité
3.3. Table de Karnaugh
3.4. Théorèmes logiques
3.1.
Définition
Un système logique est dit
combinatoire si l'état de sa sortie ne dépend
que de l'état de son entrée. Le système combinatoire
ne doit donc pas présenter de réactions de la sortie sur
l'entrée, de sorte à ce que l'état de la sortie ne
dépende pas de l'histoire du système.
A tout instant, on peut représenter logiquement
un système combinatoire en faisant une liste des entrées
et des sorties : la table de vérité.
Par exemple, la table de vérité du
décodage gray-binaire sur 3 bits est donnée par :
|
Code gray (entrée)
|
Code binaire (sortie)
|
|
000
|
000
|
|
001
|
001
|
|
011
|
010
|
|
010
|
011
|
|
110
|
111
|
|
100
|
101
|
|
101
|
110
|
|
111
|
100
|
3.2.
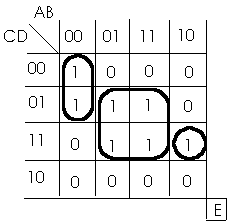
Table de Karnaugh
Cette forme de représentation est utilisée pour trouver
une expression simplifiée d'une fonction logique. Dans le cas d'un
système à quatre variables d'entrée, on crée
un tableau à 2 x 4 entrées, puis on regroupe les termes adjacents.
Par exemple, soit la table de vérité suivante :
|
ABCD
|
E
|
|
0000
|
1
|
|
0001
|
1
|
|
0010
|
0
|
|
0011
|
0
|
|
0100
|
0
|
|
0101
|
1
|
|
0110
|
0
|
|
0111
|
1
|
|
1000
|
0
|
|
1001
|
0
|
|
1010
|
0
|
|
1011
|
1
|
|
1100
|
0
|
|
1101
|
1
|
|
1110
|
0
|
|
1111
|
1
|
La résolution par Karnaugh donne :
Notez que les lignes 2,3 et les colonnes 2,3 présentent
une variable. C'est ainsi que le regroupement du centre s'écrit
: 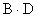 .
.
Le regroupement d'en haut à droite représente
une simplification moindre : 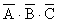 .
.
On obtient pour l'expression de la sortie :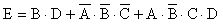
3.3.
Théorèmes logiques
Les théorèmes suivants permettent d'effectuer
des calculs dans l'algèbre de Boole :
* Théorèmes de commutativité
:
* Théorèmes d'idempotence
:
* Théorèmes des constantes
:
* Théorèmes de complémentation
:
* Théorèmes de distributivité
:
* Théorèmes de De Morgan :
[ Table des matières ]
![]()