
______________________________________________________
LE TRANSISTOR MOS, FAMILLES LOGIQUES
Bien qu'apparemment le fonctionnement du transistor MOS soit similaire à celui de son cousin bipolaire, le détail de l'analyse de son fonctionnement laisse apparaître de grandes divergences qui l'ont promulgué candidat unique à l'intégration des circuits intégrés numériques. On donne quelques exercices simples destinés à se familiariser avec le fonctionnement du MOS, ainsi qu'une courte information sur les familles technologiques.
____________________________________________________
Table des matières
| 1. Généralités 1.1. Introduction 1.2. Définitions 1.3. Description 1.4. Commentaire |
2. Fonctionnement
du transistor MOS 2.1. Introduction 2.2. Définitions 2.3. Flat-Band 2.4. Forte inversion 2.5. Conduction 2.6. Saturation |
| 3. Charges
et canal 3.1. Introduction 3.2. Définitions 3.3. Description 3.4. Définitions 3.5. Modèle 3.6. Définition |
4. Courants
dans le MOS 4.1. Introduction 4.2. Description 4.3. Définitions 4.4. Représentation 4.5. Définitions 4.6. Représentations 4.7. Modulation de la longueur du canal 4.8. Modèle pour accroissements |
| 5. Introduction
aux familles technologiques 4.1. La logique des diodes 4.2. La logique des transistors bipolaires 4.3. La logique des transistors MOS |
6. Caractéristiques
importantes (Critères de selection) 5.1. Caractéristiques de transfert 5.2. Fan-In et Fan-Out 5.3. Puissance dissipée 5.4. Délais de propagation par porte 5.5 Produit puissance-délai |
_________________________________________________________________
____________________________________
______________________________________________________
1. GENERALITES
_____________
1.1. Introduction
1.2. Définitions
1.3. Description
1.4. Commentaire
En 1930, L. Lilienfeld de l'Université de Leipzig dépose un brevet dans lequel il décrit un élément qui ressemble au transistor MOS (Métal Oxyde Semiconducteur) actuel. Cependant, ce n'est que vers 1960 que, la technologie ayant suffisamment évolué, de tels transistors peuvent être réalisés avec succès. En particulier, les problèmes d'interface oxyde-semiconducteur ont pu être résolus grâce à l'affinement de la technologie dans le domaine bipolaire, affinement requis pour obtenir des transistors de meilleure qualité. Aujourd'hui le transistor MOS constitue, par sa simplicité de fabrication et ses petites dimensions, l'élément fondamental des circuits intégrés numériques à large échelle.

Figure 1: structures et symboles des transistors MOS
Le transistor MOS est un transistor à effet de champ constitué
d'un substrat semiconducteur (B) recouvert d'une couche d'oxyde sur laquelle
est déposée l'électrode de grille (G). Par le biais
d'une différence de potentiel appliquée entre grille et substrat,
on crée, dans le semiconducteur, un champ électrique qui
a pour effet de repousser les porteurs majoritaires loin de l'interface
oxyde-semiconducteur et d'y laisser diffuser des minoritaires venus de
deux îlots de type complémentaire au substrat, la source (S)
et le drain (D). Ceux-ci forment une couche pelliculaire de charges mobiles
appelée canal. Ces charges sont susceptibles de transiter entre
le drain et la source situés aux extrémités du canal
(fig. 1). Dans cette même figure, on a également représenté
les symboles des transistors MOS à canal n et à canal p.
La flèche indique le sens de conduction des jonctions substrat-source
(BS) et substrat-drain (BD). Sauf près de l'interface oxyde-semiconducteur,
ces jonctions sont polarisées en sens inverse. A la figure 2, on
a représenté différents symboles couramment utilisés
pour les transistors MOS.

Figure 2: différents symboles du MOS
La longueur du canal est la distance L, comptée selon l'axe y, entre
la jonction substrat-source et la jonction substrat-drain.
La largeur du canal, w, correspond à la largeur, selon l'axe z, des îlots semiconducteurs formant la source et le drain (fig. 3).
On intègre des transistors MOS de type complémentaires (CMOS) dans un même substrat. Les transistors à canal n sont intégrés directement dans le substrat de type p et on réalise un caisson d'isolation de type n dans lequel sont intégrés les transistors à canal p (fig. 4). Pour satisfaire la polarisation inverse des jonctions BS et BD, le caisson de type n est connecté au potentiel le plus positif et le substrat de type p au potentiel le plus négatif. Il est intéressant de remarquer que le transistor est déterminé par l'emplacement de la grille (sur l'oxyde mince).
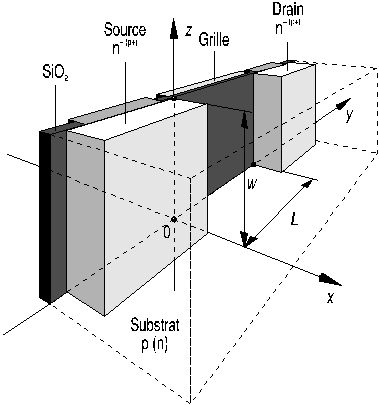
Figure 3: structure d'un transistor MOS
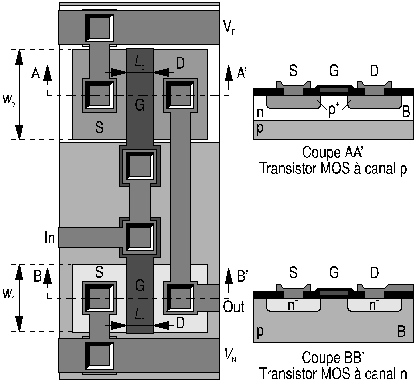
Figure 4: MOS complémentaires
Les deux technologies les plus courantes sont celles dites "à
grilles métalliques" et "à grilles polysilicium".
Dans la technologie à grilles métalliques, on utilise le même métal (généralement de l'aluminium) que celui qui permet d'interconnecter les différentes électrodes du circuit pour réaliser les grilles.
Dans la technologie à grilles polysilicium, c'est une couche de silicium polycristallin, sur l'oxyde mince, qui constitue les grilles. Lors de la diffusion des sources et des drains, cette couche masque le canal et permet de réaliser ainsi un auto-alignement des sources et des drains avec les grilles. Après l'opération de diffusion, les trois électrodes sont dopées de même façon.
Dans ce chapitre, on étudie le fonctionnement d'un transistor MOS à canal n et à substrat homogène. Le soin est laissé au lecteur de transposer les résultats pour le cas du transistor MOS à canal p (inversion de la polarité des tensions et du sens des courants).
______________________________________________________
2. FONCTIONNEMENT
DU
TRANSISTOR MOS
_____________
2.1. Introduction
2.2. Définitions
2.3. Flat-Band
2.4. Forte inversion
2.5. Conduction
2.6. Saturation
Dans cette section, on décrit le fonctionnement du transistor MOS de manière à ce que le lecteur en ait une compréhension intuitive.
Tous les potentiels sont référés à celui de l'électrode de substrat. On désigne par mode F le mode de fonctionnement dans lequel le potentiel de drain VD est différent de zéro et par mode R le mode de fonctionnement dans lequel le potentiel de source VS est différent de zéro.
On désigne par Vs la valeur particulière du potentiel à l'interface oxyde-semiconducteur. On lui donne le nom de potentiel d'interface.
La condition flat-band est déteminée par le fait que le potentiel d'interface V est nul. Dans la figure 5, on a représenté les charges dans un transistor n-MOS en condition flat-band. On remarque, en particulier, que les deux jonctions substrat-source et substrat-drain sont bloquées.
Dans la même figure, on montre le potentiel énergétique pour les électrons. On constate que, ni les électrons de la source, ni les électrons du drain, n'ont une énergie suffisante pour pénétrer dans le substrat. De même, les trous du substrat n'ont pas une énergie suffisante pour pénétrer dans les électrodes de source et de drain.
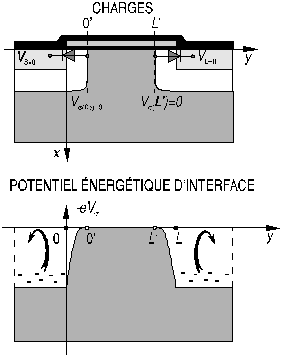
Figure 5: MOS en condition de "flat-band"
Si l'on augmente le potentiel de grille, un champ électrique va repousser les trous loin de l'interface oxyde-semicon-ducteur et le potentiel dont il découle va progressivement augmenter le potentiel d'interface (diminution du potentiel énergétique d'interface pour les électrons) jusqu'à ce que les jonctions substrat-source et substrat-drain conduisent. On admet qu'elles conduisent lorsque le potentiel à leur anode vaut Vj. Les électrons de la source, comme ceux du drain, peuvent alors passer la barrière de potentiel et se répendre le long de l'interface oxyde-semiconducteur, formant une nappe qui relie la source au drain (Fig. 6). Le trous ayant été repoussés de l'interface oxyde-semiconducteur, il n'y aura pas d'injection de trous du substrat dans les deux électrodes drain et source.
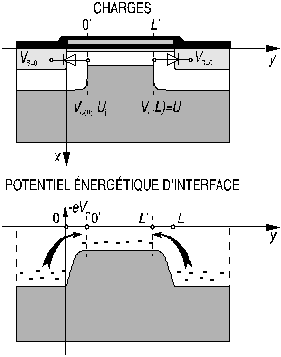
Figure 6: MOS en forte inversion, au repos
En conduction, le deux jonctions substrat-source et substrat-drain conduisent toutes les deux. Cependant, on augmente le potentiel d'une des électrodes (Drain en mode F, source en mode R), ce qui a pour conséquence de faire varier le potentiel d'interface entre la source et le drain, ce potentiel suivant les potentiel de source et de drain à une tension de jonction près aux extrémités du canal (Fig. 7). De la variation du potentiel d'interface découle un champ électrique qui aura pour effet de pousser les électrons vers une des extrémités du canal (vers le drain en mode F et vers la source en mode R).
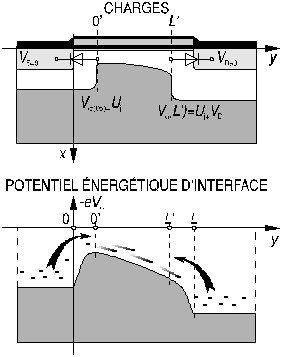
Figure 7: MOS en conduction
Le transistor MOS atteint la saturation lorsqu'on a suffisamment augmenté le potentiel de l'une des électrodes, drain (en mode F) ou source (en mode R), pour que la jonction substrat-électrode correspondante se bloque. Le flux d'électrons, et par conséquent le courant correspondant, n'est plus tributaire alors que du potentiel de l'électrode qui injecte et du potentiel de grille (Fig.8). Vu de l'électrode dont la jonction est bloquée, le transistor MOS se comporte alors comme une source de courant.
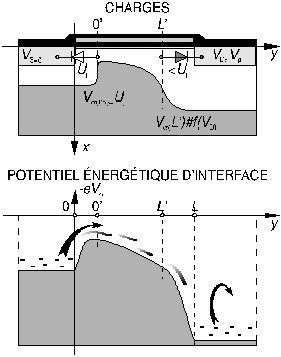
Figure 8: MOS en saturation
______________________________________________________
3. CHARGES ET
CANAL
_____________
3.1. Introduction
3.2. Définitions
3.3. Description
3.4. Définitions
3.5. Modèle
3.6. Définition
La charge des électrons qui forme le canal est appelée charge induite. La connaissance de cette charge induite permet de calculer les courants dans le transistor MOS. Par la suite, on considère les charges par unité de surface de l'interface oxyde-semiconducteur et l'on parle de charge surfacique.
On appelle capacité surfacique de l'oxyde la capacité par unité de surface C'ox du condensateur plan dont le diélectrique est constitué par l'oxyde d'épaisseur t et dont les électrodes sont la grille et le semiconducteur ([C'ox] = F/m2).
![]() (1)
(1)
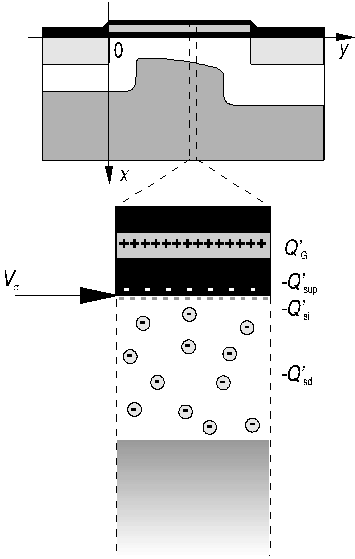
Figure 9: charges surfaciques
On appelle charge surfacique de déplétion (voir figure 9)
la charge -Q'sd constituée par les accepteurs ionisés
de la zone de déplétion située sous l'interface oxyde-semiconducteur.
On peut démontrer, en utilisant la loi de Gauss, que la charge surfacique
de déplétion dépend du potentiel d'interface par la
relation
![]() (2)
(2)
où
![]() (3)
(3)
avec [K ]= As/m2V1/2.
On appelle charge surfacique induite la charge -Q'si constituée par les électrons qui forment le canal.
On appelle charge surfacique supplémentaire une charge fictive -Q'sup que l'on situe dans l'oxyde, à proximité de l'interface oxyde-semiconducteur, et qui rend compte d'une différence de potentiel électrochimique entre grille et substrat ainsi que de différentes charges trappées dans l'oxyde. On suppose que la charge surfacique supplémentaire est constante.
On appelle charge surfacique de grille la charge positive Q'G qui se trouve sur la grille et qui neutralise toutes les charges négatives que l'on trouve du côté semiconducteur.
Le bilan des charges surfaciques s'écrit:
![]() (4)
(4)
avec
![]() (5)
(5)
et
![]() (6)
(6)
La figure 10 montre l'évolution de ces différentes charges
en fonction du potentiel d'interface Vs . On
y met en évidence la charge surfacique induite Q'si qui
a pour expression:
![]() (7)
(7)
On appelle potentiel de seuil nominal VT0 le potentiel de grille pour lequel, alors que les potentiels de source et de drain sont nuls, le potentiel d'interface Vs atteint Vj , c'est-à-dire le potentiel de grille qui entraîne la forte inversion à l'interface oxyde-semiconducteur. On obtient l'expression de VT0 en annulant Q'si et en posant Vs = Vj dans (7).
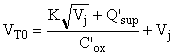 (8)
(8)
Pour simplifier les calculs en forte inversion, on admet une variation linéaire de la charge surfacique de déplétion avec Vs dès que Vs > Vj (fig. 10):
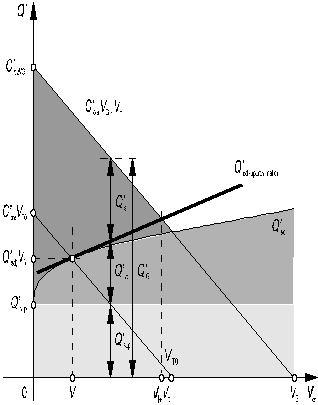
Figure 10: charges dans un MOS en fonction du potentiel d'interface
![]() (9)
(9)
avec
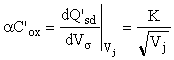 (10)
(10)
et
![]() (11)
(11)
En posant n0 = 1+a , la charge surfacique induite peut alors être exprimée par la relation:
![]() (12)
(12)
A VG donné, on constate que la charge surfacique induite s'annule lorsque le potentiel de surface atteint la valeur:
![]() (13)
(13)
Le potentiel Vp est appelé potentiel de pincement.
______________________________________________________
4. COURANTS DANS
LE MOS
_____________
4.1. Introduction
4.2. Description
4.3. Définitions
4.4. Représentation
4.5. Définitions
4.6. Représentations
4.7. Modulation de la longueur du canal
4.8. Modèle pour accroissements
Le courant traversant un MOS en forte inversion est dû à l'influence d'un champ électrique Ey, imposé par les potentiels de drain et de source, qui entraîne à une vitesse vn = - mnEy la charge induite formant le canal. Le courant de drain, positif lorsqu'il traverse le MOS du drain à la source, est égal au débit des charges formant le canal.
La charge dQsi = Q'si× w× dy située dans une tranche de longueur dy et de largeur w s'écoule à travers la section du canal en un temps dt = dy/vn On peut ainsi exprimer le courant par la relation
![]() (14)
(14)
Introduisant la vitesse
![]() (15)
(15)
dans (14), on obtient une équation différentielle à variables séparables qu'il suffit d'intégrer sur toute la longueur du canal pour pouvoir exprimer le courant drain:
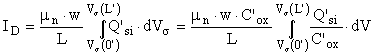 (16)
(16)
On appelle paramètre de transconductance la grandeur b ([b] = A/V2), dépendant de la technologie, définie par la relation:
![]() (17)
(17)
Il faut encore remarquer que, pour autant que le canal ne soit pas pincé, on peut écrire (voir figure 7):
![]() (18)
(18)
et
![]() (19)
(19)
Si l'on pose encore:
![]() (20)
(20)
on peut écrire (16) sous la forme
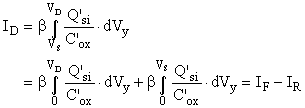 (21)
(21)
On appelle mode F le mode de fonctionnement particulier définit par VS = 0. Le courant en mode F s'écrit:
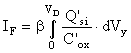 (22)
(22)
On appelle mode R le mode de fonctionnement particulier définit par VD = 0. Le courant en mode R s'écrit:
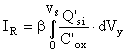 (23)
(23)
En tenant compte des considérations ci-dessus, on peut simplifier considérablement la figure 10 et représenter Q'si/C'ox en fonction de Vy (figure 11).
Le courant IX dans un mode quelconque (X) est proportionnel à la suface du trapèze grisé de la figure 11. On constate que ce courant croît en fonction de VX jusqu'au potentiel de pincement Vp selon la relation:
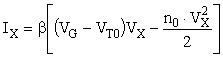 (24)
(24)
Dès que VX devient supérieur à Vp, le courant IX reste constant et a pour expression:
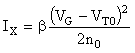 (25)
(25)
Ces relations sont représentées par les caractéristiques de sortie de la figure 12.
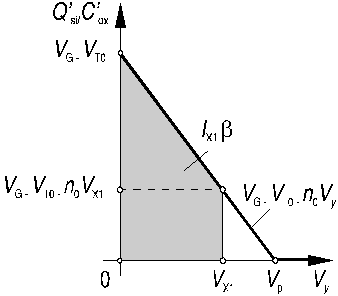
Figure 11: représentation des courants dans le MOS
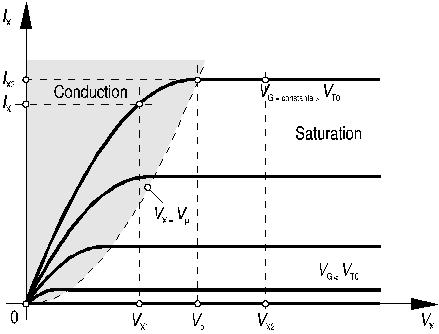
Figure 12: caractéristiques de sortie du transistor MOS
On appelle conduction le régime de fonctionnement dans lequel le pincement n'apparaît pas dans le canal, c'est-à-dire lorsque VD < Vp et VS < Vp.
Le courant drain ID = IF - IR s'écrit alors:
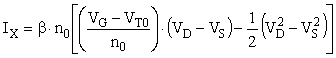 (26)
(26)
On appelle saturation directe le régime de fonctionnement dans lequel il y a pincement à l'extrémité drain du canal uniquement, c'est-à-dire lorsque VD ³ Vp et VS < Vp. Le courant de drain a pour expression:
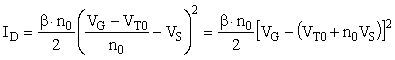 (27)
(27)
On appelle saturation inverse le régime de fonctionnement dans lequel il a pincement à l'extrémité source du canal uniquement, c'est-à-dire lorsque VD < Vp et VS ³ Vp. Le courant de drain s'écrit:
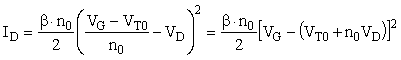 (28)
(28)
Dans les régimes de saturation, on constate que le courant de drain est indépendant du potentiel de drain en saturation directe et du potentiel de source en saturation inverse; par conséquent, le MOS se comporte comme une source de courant idéale commandée par le potentiel VG. A la figure 13, on a représenté la caractéristique de transfert du MOS.
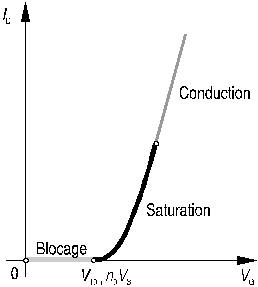
Figure 13: caractéristique de transfert
Si les potentiels de drain ou de source ne sont pas nuls, tout se passe comme si le potentiel de seuil avait varié pour prendre la valeur:
![]() (29)
(29)
On parle souvent de modulation du potentiel de seuil par le substrat car c'est parce que la source (ou le drain) n'est pas au potentiel du substrat que le phénomène se produit.
Finalement on appelle blocage le régime de fonctionnement dans lequel il y a pincement aux deux extrémités du canal et par conséquent dans tout le canal. Aucun courant ne peut alors circuler:
![]() (30)
(30)
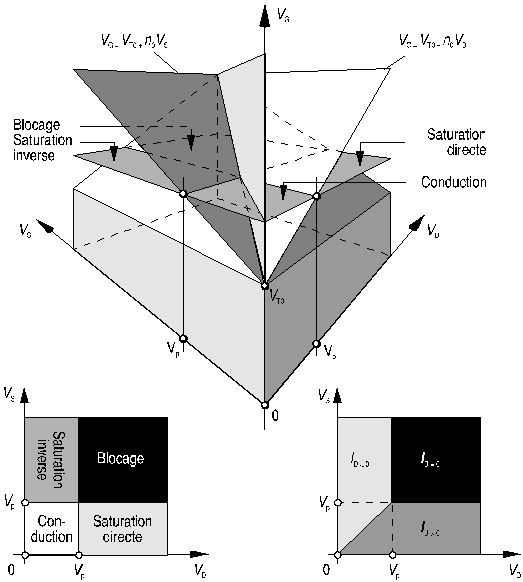
Figure 14: régimes de fonctionnement du transistor MOS
Pour une valeur donnée du potentiel de grille, les divers régimes de fonctionnement peuvent être illustrés par des surfaces dans le plan (VD, VS) (fig. 14).
Il faut encore remarquer que le courant ID, hors du blocage, est positif si VD > VS, négatif si VD < VS et nul si VD = VS.
4.7. Modulation
de la longueur du canal
Au paragraphe 4.6, on a admis que le transistor MOS se comportait comme une source de courant idéale en régime de saturation. En réalité, l'extrémité effective L' du canal varie en fonction du potentiel de drain que l'on applique. Si l'on appelle ID0 la valeur théorique du courant de drain en saturation directe donnée par la relation (27), on admet qu'en tenant compte de l'effet de modulation de la longueur du canal, le courant de drain s'écrit:
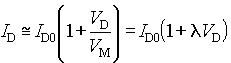 (31)
(31)
l et VM sont indifféremment appelés paramètres de modulation de la longueur du canal. La figure 15 montre des caractéristiques de sortie du transistor MOS qui tiennent compte de la modulation de la longueur du canal.
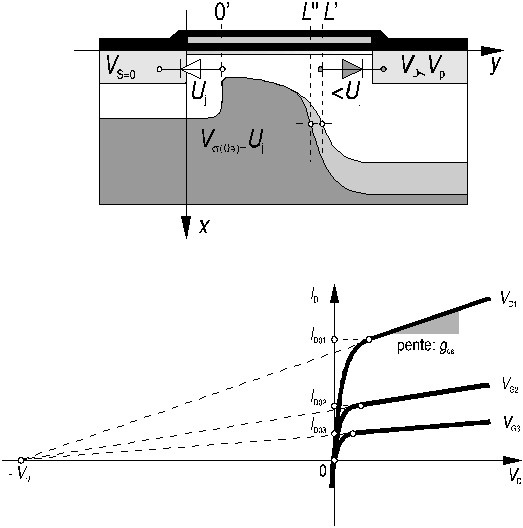
Figure 15: effet de la modulation de la longueur du canal
4.8. Modèle
pour accroissements
On suppose, pour la suite de notre étude, qu'en régime d'accroissements le transistor MOS travaille autour d'un point de repos Pq qui le met en saturation directe et que le potentiel de source est constant. Les accroissements du courant de drain sont commandés par les accroissements des potentiels de grille et de drain selon la relation:
![]() (32)
(32)
où
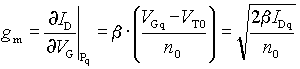 (33)
(33)
et
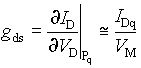 (34)
(34)
A la figure 16, on a représenté le schéma équivalent pour accroissements du transistor MOS. Par la structure même du composant, on conçoit que la grille est liée capacitivement à la source, au drain et au substrat et que le drain est lié au substrat par la capacité de transition de la jonction substrat-drain polarisée en sens inverse.
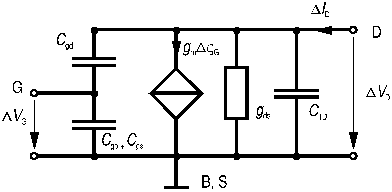
Figure 16: modèle pour accroissements
______________________________________________________
5. FAMILLES
TECHNOLOGIQUES :
INTRODUCTION
_____________
5.1. La logique à diodes
5.2. La logique à transistors bipolaires
5.3. La logique à transistors MOS
Ici, on montre une logique à diodes, une logique à transistors bipolaire et un étage de sortie à transistors MOS à titre d'illustration générale. Quelques caractéristiques de circuits intégrés logiques sont présentées.
Idéalement, la valeur logique "0"
s'incarne électroniquement en une tension de 0 Volt, et la valeur
logique "1" en une tension de +Vcc, soit le niveau
de l'alimentation.
5.1.
La logique à diodes
Elle utilise ces éléments
passifs pour réaliser les fonctions logiques précitées.
Cette technologie n'est (presque) plus utilisée.
L'analyse du dispositif logique à diodes suivant est laissée en exercice :
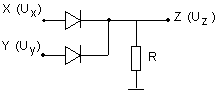
5.2. La
logique à transistors bipolaires
Elle porte le nom générique de logique TTL. Elle fonctionne normalement sous une tension d'alimentation de 5 V, et est encore très utilisée.
On invite l'étudiant à analyser l'inverseur logique à transistor bipolaire suivant :
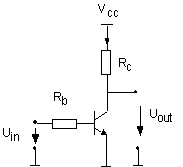
5.3. La
logique à transistors MOS
Elle porte ce nom générique (MOS, CMOS,
HCMOS, ...). Elle est généralement plus lente que la logique
bipolaire, mais elle consomme moins de courant sur l'alimentation. (Cf.
TP). Cette consommation étant due essentiellement aux capacités
internes, elle augmente avec la fréquence de travail.
Soit ce montage de base, pour un étage de sortie CMOS :
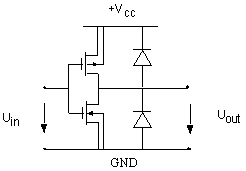
6.
CARACTÉRISTIQUES IMPORTANTES (CRITÈRES
DE SÉLECTION)
_____________
6.1. Caractéristiques de transfert
6.2. Fan-In et Fan-Out
6.3. Puissance dissipée
6.4. Délais de propagation par porte
6.5 Produit puissance-délai
6.1.
Caractéristiques
de transfert
Il va de soi que la caractéristique
de transfert en tension ne peut pas être fixée absolument
pour un type de circuit donné. On spécifie cette donnée
sous forme de tolérances :
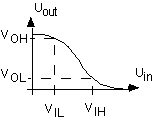

Marges de bruit :
Comme la sortie d'un circuit logique est souvent connectée à l'entrée d'un autre, deux grandeurs pertinentes sont la marge de bruit et la marge de tension parasite que peut supporter la transmission, sans subir d'erreur logique :
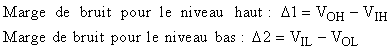
Ces marges de bruit sont bien sûr spécifiées pour des familles logiques, avec des tensions d'alimentation. L'interfaçage de différentes familles logiques ne peut donc se faire sans précautions particulières quant à ces marges, et plus généralement quant à l'ensemble des caractéristiques des familles concernées.
Pour un circuit donné, le fabricant spécifie le nombre de circuits du même type que l'on peut placer en amont et en aval, sans détériorer les performances du système :
Fan-in : nombre maximum de portes pouvant débiter dans le circuit :
Fan-out: nombre maximum de portes pouvant charger le circuit.
Exemple: La porte OU du montage ci-dessous est chargée par deux portes et charge une seule porte :
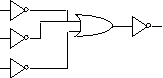
Remarquons que les sorties d'inverseurs mises ensembles
doivent être à collecteur ouvert, sinon on assiste à
des court-circuits ou des indéterminations.
6.3.
Puissance dissipée
Que ce soit pour les circuits logiques ou analogiques, intégrés ou pas, la puissance dissipée est toujours un paramètre important.
* L'alimentation des circuits doit être capable de débiter le courant nécessaire.
Exemple: un système logique consomme en moyenne 100 mA sous une tension d'alimentation de 5 V. Quelle est la puissance moyenne nécessaire au fonctionnement du système ? Combien de temps une batterie de 5V spécifiée 1 A h (Ampère fois heure) peut-elle remplir son rôle ?
* Le circuit qui est le siège de l'échauffement par effet Joule doit être capable d'évacuer la chaleur, pour maintenir une température de fonctionnement acceptable.
On définit le concept de résistance thermique :
Le signal de sortie d'une porte logique accuse un certain retard par rapport à la transition du signal d'entrée. Ce retard est lié à divers phénomènes dynamiques, et les fabricants spécifient les délais de propagation en mesurant les signaux à mi-tension.
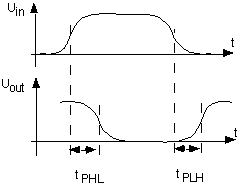
On définit le temps de propagation ![]() comme la moyenne de ces deux temps :
comme la moyenne de ces deux temps :
Au sein d'une famille logique, on peut dans certaines limites, concevoir des circuits à faible délai au prix d'une consommation élevée ou réciproquement on peut diminuer leur consommation, si on se contente de rapidités moindres.
Remarquons que l'apparition de ce type de compromis est typique en électronique, où des impédances de sortie plutôt résistives se combinent avec des capacités parasites peu contrôlées : si on diminue la résistance de sortie R, le produit RC diminue, donc la rapidité du circuit augmente. Cela peut néanmoins se faire par le biais d'une augmentation de courant, donc de consommation.
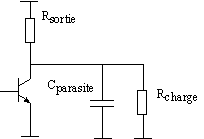
Revenons à nos circuits logiques, où pour une famille logique, le
produit Puissance * Délai est constant sur une certaine plage de puissance et/ou de délais. On peut donc utiliser ce produit comme un facteur de mérite qui caractérise la famille logique. Par exemple, il vaut :
