Dans cette partie, on présente sans l'approfondir une introduction aux semiconducteurs et à la jonction PN. La physique des semiconducteurs, tant dans sa dimension appliquée que dans sa dimension recherche technologique est bien représentée à l'École polytechnique de Lausanne. Pour les étudiants physiciens, il y a le cours de matériaux de troisième année ainsi que celui de semiconducteurs de quatrième année.
 

Ce qui importe ici est de se familiariser avec le modèle exponentiel de la diode et ses diverses simplifications dans des montages très classiques. Les exercices et le premier travail pratique du semestre y sont consacrés.  

1.1. Introduction
1.2. Description: semiconducteur intrinsèque
1.3. Description: semiconducteur extrinsèque de type n
1.4. Description: semiconducteur extrinsèque de type p
1.5. Commentaires

1.1. Introduction
Cette section, essentiellement descriptive, a pour objet de donner au lecteur des modèles simples de semiconducteurs intrinsèques et extrinsèques de type n ou de type p. La connaissance de ces modèles permet, par la suite, de rendre compte du comportement des dispositifs à semiconducteurs tels que diode, transistor bipolaire, transistors à effet de champ, etc.
 

1.2. Description: semiconducteur intrinsèque

Un cristal de semiconducteur intrinsèque est un solide dont les noyaux atomiques sont disposés aux noeuds d'un réseau géométrique régulier. La cohésion de cet édifice est assurée par les liens de valence qui résultent de la mise en commun de deux électrons appartenant chacun à deux atomes voisins de la maille cristalline. Les atomes de semiconducteur sont tétravalents et le cristal peut être représenté par le réseau de la figure 1:

 

Figure 1: semiconducteur intrinsèque

Définitions

L'électron qui possède une énergie suffisante peut quitter la liaison de valence pour devenir un électron libre. Il laisse derrière lui un trou qui peut être assimilé à une charge libre positive; en effet, l'électron quittant la liaison de valence à laquelle il appartenait démasque une charge positive du noyau correspondant. Le trou peut être occupé par un autre électron de valence qui laisse, à son tour, un trou derrière lui: tout se passe comme si le trou s'était déplacé, ce qui lui vaut la qualification de charge libre. La création d'une paire électron libre - trou est appelée génération alors qu'on donne le nom de recombinaison au mécanisme inverse.

Assertion

La température est une mesure de l'énergie cinétique moyenne des électrons dans le solide. On comprend dès lors que la concentration des électrons libres et des trous dépende très fortement de la température.

Exemples

Le silicium a un nombre volumique d'atomes de 5× 10²² par cm³. A 300K (27° C), le nombre volumique des électrons libres et des trous est de 1,5× 10¹⁰ cm^-3, soit une paire électron libre - trou pour 3,3× 10¹² atomes.

Le nombre volumique des atomes dans le germanium est de 4,4× 10²² par cm³. A 300K, le nombre volumique des électrons libres et des trous est 2,5× 10¹³ cm^-3, soit une paire électron libre - trou pour 1,8× 10⁹ atomes.

1.3. Description: semiconducteur extrinsèque de type n
Un semiconducteur dans lequel on aurait substitué à quelques atomes tétravalents des atomes pentavalents est dit extrinsèque de type n (Fig. 2)

Figure 2: semiconducteur de type n

Quatre électrons de la couche périphérique de l'atome pentavalent prennent part aux liens de valence alors que le cinquième, sans attache, est libre de se mouvoir dans le cristal. L'électron libre ainsi créé neutralise la charge positive, solidaire du réseau cristallin, qu'est l'atome pentavalent ionisé.

Définitions

Le dopage est l'action qui consiste à rendre un semiconducteur extrinsèque. Par extension, ce terme qualifie également l'existence d'une concentration d'atomes étrangers: on parle de dopage de type n. On donne le nom d'impuretés aux atomes étrangers introduits dans la maille cristalline. Dans le cas d'un semiconducteur extrinsèque de type n, les impuretés sont appelées donneurs car chacune d'entre elles donne un électron libre.

Modèle

Les dopages courants sont d'environ 10¹⁶ à 10¹⁸ atomes par cm³. On peut admettre que le nombre volumique des électrons libres est égal au nombre volumique des impuretés et que le nombre volumique des trous (charges libres positives) est négligeable. Etant données ces considérations, on établit le modèle de semiconducteur représenté à la figure 3 dans lequel n'apparaissent que les charges essentielles, à savoir: les électrons libres et les donneurs ionisés. Les charges fixes sont entourées d'un cercle.

Figure 3: semiconducteur de type n (modèle)

1.4. Description: semiconducteur extrinsèque de type p

Si l'on introduit des atomes trivalents dans le réseau cristallin du semiconducteur, les trois électrons de la couche périphérique de l'impureté prennent part aux liens de valence, laissant une place libre. Ce trou peut être occupé par un électron d'un autre lien de valence qui laisse, à son tour, un trou derrière lui. L'atome trivalent est alors ionisé et sa charge négative est neutralisée par le trou (voir fig. 4). Le semiconducteur est alors extrinsèque de type p.

Définition

Les impuretés, dans un semiconducteur extrinsèque de type p. sont appelées accepteurs au vu de leur propriété d'accepter un électron situé dans un lien de valence.

Modèle

On peut faire les mêmes considérations qu'au paragraphe 1.8 concernant le nombre volumique des trous: il est approximativement égale au nombre volumique des impuretés. Le nombre volumique des électrons libres est alors considéré comme négligeable. Il s'ensuit un modèle, représenté à la figure 5, dans lequel n'apparaissent que les charges prépondérantes: les trous et les accepteurs ionisés.

1.5. Commentaire
Il faut remarquer que le semiconducteur extrinsèque, type p ou type n, est globalement neutre. On peut le comparer à un réseau géométrique dont certains noeuds sont chargés et dans lequel stagne un gaz de charges mobiles qui neutralise les charges fixes du réseau. On élargit, par la suite, la notion de semiconducteur de type n à un semiconducteur dont le nombre volumique des donneurs l'emporte sur celui des accepteurs et celle de semiconducteur de type p à un semiconducteur dans lequel le nombre volumique des accepteurs est prépondérant.  

2.1. Introduction
2.2. Descrption
2.3. Définition
2.4. Assertion
2.5. Propriété
2.6. Exemple
2.7. Commentaire

2.1. Introduction
Le dopage non uniforme d'un semiconducteur, qui met en présence une région de type n et une région de type p, donne naissance à une jonction pn. Dans la présente section, on étudie, qualitativement, les phénomènes qui ont pour siège la jonction pn. On donne également la relation exponentielle qui lie courant et tension dans une telle jonction.    

2.2. Description
Soit le semiconducteur à dopage non uniforme de la figure 6 qui présente une région p à nombre volumique d'atomes accepteurs constant suivie immédiatement d'une région n à nombre volumique de donneurs constant également. La surface de transition entre les deux régions est appelée jonction pn abrupte. Du fait de la continuité du réseau cristallin, les gaz de trous de la région p et d'électrons de la région n ont tendance à uniformiser leur concentration dans tout le volume à disposition. Cependant, la diffusion des trous vers la région n et des électrons libres vers la région p provoque un déséquilibre électrique si bien que, dans la zone proche de la jonction, la neutralité électrique n'est plus satisfaite. On trouve, dans la région p, des atomes accepteurs et des électrons, soit une charge locale négative, et dans la région n, des atomes donneurs et des trous, soit une charge locale positive. Il s'est donc créé un dipôle aux abords de la jonction et, conjointement, un champ électrique. Une fois l'équilibre atteint, ce champ électrique est tel qu'il s'oppose à tout déplacement global de charges libres.

Figure 6: jonction pn abrupte

2.3. Définitions
La région dans laquelle la neutralité n'est pas satisfaite est appelée zone de déplétion ou zone de charge spatiale alors que les autres régions sont dites régions neutres.

Le champ électrique interne créé par le dipôle est nommé champ de rétention de la diffusion car il s'oppose à toute diffusion des charges mobiles.

2.4. Assertion
Généralement, la concentration des charges mobiles dans la zone de charge spatiale est négligeable vis-à-vis du nombre volumique des charges fixes. On idéalise cet état de fait et l'on admet qu'il n'y a pas de charges mobiles dans la zone de déplétion (voir fig. 7).

Figure 7: charges et champ électrique

2.5. Propriété 
Il existe, entre la région p et la région n, une barrière de potentiel énergétique pour les charges mobiles. L'existence de cette barrière se traduit par une différence de potentiel électrique liée au champ de rétention de la diffusion.  

Preuve

L'existence de la barrière de potentiel est mise en évidence par le travail W_p qu'il faut fournir pour faire passer un trou de la région neutre p à la région neutre n ou pour faire passer un électron en sens contraire (voir fig. 8)

Figure 8: grandeurs spécifiques dans une jonction pn


                     (1)

où F' est la force opposée à la force de Coulomb donnée, dans le cas du trou de charge +e, par l'expression:

                    (2)  

En introduisant (2) dans (1), on fait apparaître la notion de potentiel électrique:

                     (3)  

On désigne par U_B0 la hauteur de la barrière de potentiel dans une jonction à l'équilibre (voir fig. 8).

2.6. Exemple
Pour une jonction pn au silicium avec un dopage N_A = 10¹⁸ cm^-3 dans la région p et un dopage N_D = 10¹⁷ cm^-3 dans la région n, la hauteur de la barrière de potentiel à 300 K (27° C) à l'équilibre vaut 872 mV.

2.7. Commentaires
La hauteur de la barrière de potentiel à l'équilibre est telle que les trous qui sont dans la région p ont une énergie moyenne qui n'est juste pas suffisante pour leur permettre de passer la barrière de potentiel. Il en va de même pour les électrons qui se trouvent dans la région n.

3.1. Description
3.2. Définition
3.3. Propriétés
3.4. Définitions
3.5. Commentaires

3.1. Description

Si l'on applique une tension U à la jonction, cette tension se reporte presque entièrement à la zone de déplétion qui présente une résistivité très grande vu la quasi-absence de charges mobiles. Une tension U négative (voir fig. 9) renforce le champ de rétention de la diffusion et augmente, par conséquent, la hauteur de la barrière de potentiel, de telle sorte qu'aucune charge libre ne traverse la zone de charge spatiale.

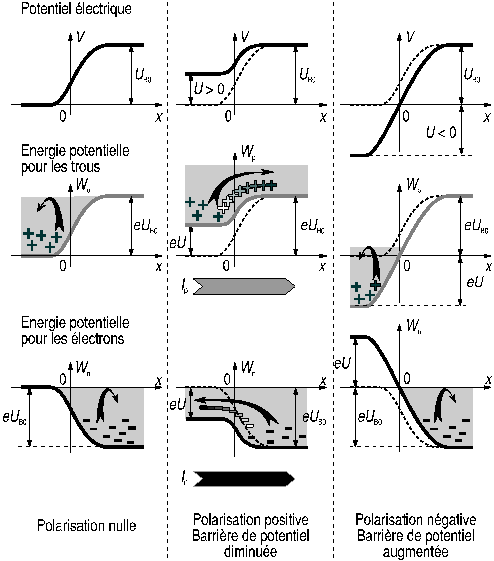
Figure 9: polarisation de la jonction

Au contraire, si l'on applique une tension U positive (voir fig. 9), le champ électrique de rétention de la diffusion est diminué et les charges mobiles qui ont une énergie supérieure à celle que représente la hauteur de la barrière de potentiel peuvent traverser la zone de charge spatiale.

Il est utile, ici, de se rappeler que l'énergie moyenne des charges mobiles est liée à la notion de température (voir § 1.4) et qu'à température donnée, cette énergie est constante.

3.2. Définitions
L'application d'une tension qui diminue la hauteur de la barrière de potentiel par rapport à l'équilibre est appelée polarisation directe par opposition à la polarisation inverse qui augmente la hauteur de la barrière de potentiel par rapport à l'équilibre.

3.3. Propriété
Une polarisation directe permet le passage d'un courant électrique dans la jonction alors qu'une polarisation inverse l'empêche. Cette propriété est traduite par les relations:

                     (4)

                       (5)

soit

                    (6)

où

                    (7)

dont la dérivation sort du cadre de cette étude. La loi exprimée par la relation (6) est représentée à la figure 10.

3.4. Définitions
Le courant I_s est appelé courant inverse de saturation; c'est la valeur asymptotique du courant I en polarisation inverse.

On appelle tension thermodynamique la tension U_T qui vaut

                     (8)

où k est la constante de Boltzmann, T la température absolue et e la charge de l'électron. A 25° C, U_T = 25mV.

Le facteur n est appelé coefficient d'émission. Il est voisin de 1 dans les jonctions de transistors au Si et dans les diodes au Ge. Il est compris entre 1 et 2 dans le cas de diodes au Si.

Figure 10: caractéristique de la jonction

3.5. Commentaires
Le courant inverse de saturation des jonctions au Silicium est de l'ordre de grandeur de 10^-12 à 10^-15 A de telle sorte qu'on peut généralement le considérer comme nul en polarisation inverse.

Figure 11: caractéristique de la jonction

Dans les cas pratiques, U >> nU_T, la relation (6) peut se mettre sous la forme approchée:

                    (9)  

La représentation semi-logarithmique de la figure 11 fait apparaître l'erreur commise en utilisant la relation (9) plutôt que (6).

A courant constant, la tension à la jonction décroît de 2 mV pour une augmentation de température de 1° C (voir fig. 10). On appelle coefficient de température la grandeur g q qui rend compte de ce phénomène:

                     (10)

où g q = -2 mV /° C.

4.1. Introduction
4.2. Assertion
4.3. Définition
4.4. Description
4.5. Remarque

4.1. Introduction

La largeur de la zone de déplétion dépend de la hauteur de la barrière de potentiel et, par conséquent, de la tension appliquée. Or, pour varier les dimensions de cette zone, on doit introduire ou retirer des charges mobiles qui neutralisent les charges fixes des atomes ionisés. Dans la description de la jonction en régime dynamique, on traduit ce comportement capacitif par la notion de capacité de transition.

4.2. Assertion
La largeur l de la zone de déplétion suit la loi:

                     (11)

dans laquelle le paramètre m est compris entre 1/3, pour une jonction progressive linéaire, et 1/2, pour une jonction abrupte.

4.3. Définition
Soit Q_T la charge de la zone de déplétion dans la région neutre n. Un accroissement dU_B de la hauteur de la barrière de potentiel, égal à l'accroissement dU de tension appliqué à la jonction, provoque un accroissement dQ_T de la charge Q_T (voir figure 12).

Figure 12: capacité de transition

On appelle capacité de transition la capacité différentielle définie par la relation:

                     (12)

4.4. Description
Comme pour tout condensateur plan, la capacité de transition se calcule d'après la relation:

                     (13)

ou e est la permittivité du semiconducteur, A la section de la jonction et l la largeur de la zone de déplétion.

Comme la largeur de la zone de déplétion dépend de la tension U appliquée (12), la capacité de transition varie également en fonction de U selon la relation:

                     (14)

où C_T0 est la capacité de transition à tension nulle; elle a pour expression:

                     (15)

A la figure 13, on a représenté l'allure de la capacité de transition en fonction de la tension appliquée à la jonction.

Figure 13: capacité de transition

4.5. Remarque
Dans les diodes dites VARICAP, on utilise la propriété de variation de la capacité de transition en fonction de la tension moyenne appliquée. On a recours à de tels éléments en radio, par exemple, pour réaliser des circuits oscillants dont la fréquence de résonance est réglée au moyen d'une tension.